题目内容
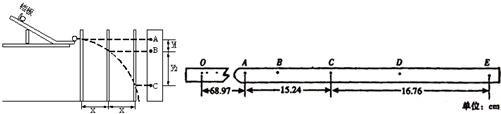
在利用电磁打点计时器（所用电源的频率为50Hz）“验证机械能守恒定律”的实验中：（1）某同学用图甲所示的装置进行实验，得到如图乙所示的纸带，把第一个点（初速度为零）记作O点，测出点O、A间的距离为68.97cm，点A、C间的距离为15.24cm，点C、E间的距离为16.76cm，已知当地的重力加速度为9.80m/s2，重锤的质量为1.00kg，则打点计时器在打O点到C点的这段时间内，重锤动能的增加量为______J（保留三位有效数字），重力势能的减少量为______J（保留三位有效数字）；
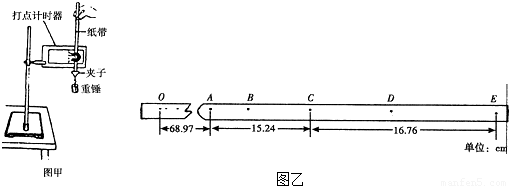
（2）利用这个装置还可以测量出重锤下落的加速度a=______m/s2；
（3）在实验中发现，重锤减小的重力势能总大于重锤增大的动能，其原因主要是因为在重锤带着纸带下落的过程中存在着阻力的作用，用题目中的相关数据可以求出重锤下落过程中受到的平均阻力大小为______N．
【答案】分析：（1）根据某段时间内的平均速度等于中间时刻的瞬时速度求出C点的瞬时速度，从而得出C点的动能，知道重锤动能的增加量．根据重力做功求出重力势能的减小量．
（2）根据连续相等时间内的位移之差是一恒量，即△x=aT2求出重锤下落的加速度．
（3）重锤受重力和阻力，根据牛顿第二定律列式求解．
解答：解：（1）C点的速度等于AE段的平均速度，vC=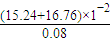
m/s=4m/s，
则动能的增加量△Ek=
mvC2=
×1×16J=8.00J
重力势能的减小量△Ep=mgh=9.8×（68.97+15.24）×10-2=8.25J．
（2）根据△x=aT2得，a=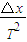
=
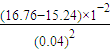m/s2=9.5m/s2．
（3）根据牛顿第二定律，有：mg-f=ma
解得：f=m（g-a）=1×（9.8-9.5）=0.3N
故答案为：（1）8.00；8.25；（2）9.5；（3）0.3．
点评：解决本题的关键掌握动能变化量和重力势能的变化量的求法，能够灵活运用运动学推论和牛顿第二定律进行求解．
（2）根据连续相等时间内的位移之差是一恒量，即△x=aT2求出重锤下落的加速度．
（3）重锤受重力和阻力，根据牛顿第二定律列式求解．
解答：解：（1）C点的速度等于AE段的平均速度，vC=
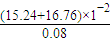m/s=4m/s，则动能的增加量△Ek=
mvC2=×1×16J=8.00J重力势能的减小量△Ep=mgh=9.8×（68.97+15.24）×10-2=8.25J．
（2）根据△x=aT2得，a=
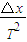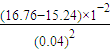=m/s2=9.5m/s2．（3）根据牛顿第二定律，有：mg-f=ma
解得：f=m（g-a）=1×（9.8-9.5）=0.3N
故答案为：（1）8.00；8.25；（2）9.5；（3）0.3．
点评：解决本题的关键掌握动能变化量和重力势能的变化量的求法，能够灵活运用运动学推论和牛顿第二定律进行求解．
练习册系列答案
相关题目
