题目内容
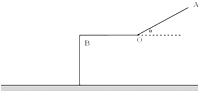
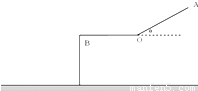
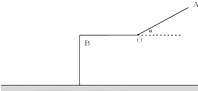滑雪运动员从A点由静止沿倾角为 θ 的斜面滑下，经一平台后水平飞离B点，B点离地高度为 H，斜面、平台与滑雪板之间的动摩擦因数均为 μ．OA=OB=L，假设滑雪者由斜面底端进入平台后立即沿水平方向运动，且速度大小不变．求：（1）滑雪者在斜面上的加速度的大小．
（2）滑雪者离开 B 点时的速度大小．
（3）滑雪者的落地点与 B 点的水平距离．
分析：（1）对运动员受力分析，受重力、支持力和滑动摩擦力，根据牛顿第二定律列式求解；
（2）根据动能定理研究A到B的过程，求出滑雪者离开B点时的速度大小；
（3）滑雪者离开B点到着地过程，只受重力，是平抛运动，根据平抛运动的分位移公式列式求解．
（2）根据动能定理研究A到B的过程，求出滑雪者离开B点时的速度大小；
（3）滑雪者离开B点到着地过程，只受重力，是平抛运动，根据平抛运动的分位移公式列式求解．
解答：解：（1）滑雪者在斜面上滑动过程，对运动员受力分析，受重力、支持力和滑动摩擦力，
根据牛顿第二定律，有：mgsinθ-μmgcosθ=ma；
解得：a=g（sinθ-μcosθ）；
（2）A到B的过程，由动能定理得
mgLsinθ-μmgcosθL-μmgL=
mv2；
解得：v=
；
故滑雪者离开B点时的速度为
；
（3）雪者离开B点到着地过程，只受重力，是平抛运动，根据平抛运动的分位移公式，有：
x=vt
H=
gt2
联立解得：x=2
；
答：（1）滑雪者在斜面上的加速度的大小为g（sinθ-μcosθ）．
（2）滑雪者离开B点时的速度大小为
．
（3）滑雪者的落地点与 B 点的水平距离为2
．
根据牛顿第二定律，有：mgsinθ-μmgcosθ=ma；
解得：a=g（sinθ-μcosθ）；
（2）A到B的过程，由动能定理得
mgLsinθ-μmgcosθL-μmgL=
| 1 |
| 2 |
解得：v=
| 2gL(sinθ-μcosθ-μ) |
故滑雪者离开B点时的速度为
| 2gL(sinθ-μcosθ-μ) |
（3）雪者离开B点到着地过程，只受重力，是平抛运动，根据平抛运动的分位移公式，有：
x=vt
H=
| 1 |
| 2 |
联立解得：x=2
| HL(sinθ-μcosθ-μ) |
答：（1）滑雪者在斜面上的加速度的大小为g（sinθ-μcosθ）．
（2）滑雪者离开B点时的速度大小为
| 2gL(sinθ-μcosθ-μ) |
（3）滑雪者的落地点与 B 点的水平距离为2
| HL(sinθ-μcosθ-μ) |
点评：本题关键分析清楚运动员的运动规律，然后分阶段选择恰当的规律列式求解，不难．
练习册系列答案
华东师大版一课一练系列答案
相关题目
高台滑雪以其惊险刺激而闻名，运动员在空中的飞跃姿势具有很强的观赏性．某滑雪轨道的完整结构可以简化成如图所示的示意图．其中AB段是助滑雪道，BC段是水平起跳台，CD段是着陆雪道，AB段与BC段圆滑相连，DE段是一小段光滑的圆弧（即运动员在D点和E点速度大小相等），在D、E两点分别与CD、EF相切，EF是减速雪道，倾角θ=37°．轨道各部分与滑雪板间的动摩擦因数均为μ=0.25，C点与D点的距离为32.625m．运动员连同滑雪板的质量m=60kg，滑雪运动员从A点由静止开始起滑，通过起跳台从C点以10m/s的速度水平飞出，在落到着陆雪道上时，运动员靠改变姿势进行缓冲使自己只保留沿着陆雪道的分速度而不弹起． 除缓冲外运动员均可视为质点，设运动员在全过程中不使用雪杖助滑，忽略空气阻力的影响，取重力加速度g=10m/s2，sin37°=0.6，cos37°=0.8．求：
高台滑雪以其惊险刺激而闻名，运动员在空中的飞跃姿势具有很强的观赏性．某滑雪轨道的完整结构可以简化成如图所示的示意图．其中AB段是助滑雪道，倾角
