��Ŀ����
18��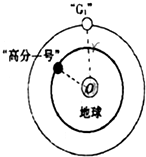 ��ͼΪ���߷�һ�š������뱱������ϵͳ�еġ�G1�����ǣ��ڿ���ijһƽ�����Ƶ���O������Բ���˶���ʾ��ͼ����֪���ǡ�G1���Ĺ���뾶Ϊr�����������������ٶ�Ϊg������뾶ΪR��������������ΪG��������
��ͼΪ���߷�һ�š������뱱������ϵͳ�еġ�G1�����ǣ��ڿ���ijһƽ�����Ƶ���O������Բ���˶���ʾ��ͼ����֪���ǡ�G1���Ĺ���뾶Ϊr�����������������ٶ�Ϊg������뾶ΪR��������������ΪG��������| A�� | ���߷�һ�š��ļ��ٶȴ������ǡ�G1���ļ��ٶ� | |
| B�� | ���߷�һ�š��������ٶȴ��ڵ�һ�����ٶ� | |
| C�� | ���������Ϊ$\frac{g{r}^{2}}{G}$ | |
| D�� | ���ǡ�G1��������Ϊ$\frac{2��r}{R}$$\sqrt{\frac{r}{g}}$ |
���� �����Ƶ�����Բ���˶������������ṩ��������Ӧ������������ʽ��ţ�ٵڶ�����������ٶȡ����ٶȡ����ڣ�Ȼ����⣮
��� �⣺A�����������ṩ����������ţ�ٵڶ����ɵã�G$\frac{Mm}{{r}^{2}}$=ma����ã�a=$\frac{GM}{{r}^{2}}$����ͼʾ��֪�����߷�һ�š��İ뾶С�����ǡ�G1���İ뾶���߷�һ�š��ļ��ٶȴ������ǡ�G1���ļ��ٶȣ���A��ȷ��
B�����������ṩ����������ţ�ٵڶ����ɵã�G$\frac{Mm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$����ã�v=$\sqrt{\frac{GM}{r}}$�����߷�һ�š��Ĺ���뾶���ڵ���뾶���߷�һ�š������ٶ�С�ڵ�һ�����ٶȣ���B����
C���������������ܵ�������������������������G$\frac{Mm}{{R}^{2}}$=mg����ã������������M=$\frac{g{R}^{2}}{G}$����C����
D�����������ṩ����������ţ�ٵڶ����ɵã�G$\frac{Mm}{{r}^{2}}$=m$��\frac{2��}{T}��^{2}$r����ã�T=$\frac{2��r}{R}$$\sqrt{\frac{r}{g}}$����D��ȷ��
��ѡ��AD��
���� ���⿼���������������ɵ�Ӧ�ã�֪�����������ṩ��������Ӧ������������ʽ��ţ�ٵڶ����ɿ��Խ��⣬ע��ƽ������Ӧ�ã�

 Сѧ��10���ӿ������100��ϵ�д�
Сѧ��10���ӿ������100��ϵ�д� �����������ĵ��ݿɴ���ǧ��������һ�ּ������������ʹ���װ�ã���;�㷺���������������ϵ���3V�Ĺ�����ѹʱ���ڿ����缫�ĵ��Һ�����ϲ�����缫�����෴�ĵ�ɲ��������Ӱ������ϣ��γ�����ʵ�ϵĵ������Ķ��Ե缫��ÿ�Ե缫�����������dz�С��ֻ�м����ף�ͬʱ����̿��缫���Ի�ü���ĵ缫��������ɴ˿�֪�����������������ԭ���ǣ�������
�����������ĵ��ݿɴ���ǧ��������һ�ּ������������ʹ���װ�ã���;�㷺���������������ϵ���3V�Ĺ�����ѹʱ���ڿ����缫�ĵ��Һ�����ϲ�����缫�����෴�ĵ�ɲ��������Ӱ������ϣ��γ�����ʵ�ϵĵ������Ķ��Ե缫��ÿ�Ե缫�����������dz�С��ֻ�м����ף�ͬʱ����̿��缫���Ի�ü���ĵ缫��������ɴ˿�֪�����������������ԭ���ǣ�������| A�� | ������ѹ�� | |
| B�� | ÿ����ʵ�缫�������缫�����dz�С | |
| C�� | ��������̿�缫���úܽ� | |
| D�� | ����̿�缫�ı�����dz��� |
| A�� | �����˶����Ƿ��ӵ������˶� | B�� | �����˶���Һ����ӵ������˶� | ||
| C�� | �¶�Խ�ߣ������˶�Խ���� | D�� | ��00C�Ļ����У������˶���ʧ |
 �����ʵ�A��B��ͬһλ���ɾ�ֹ��ʼ����ͬ����ͬʱ��ʼ��ֱ���˶������˶���v-tͼ����ͼ��ʾ����A��B�˶�����ķ��������н�����ȷ���ǣ�������
�����ʵ�A��B��ͬһλ���ɾ�ֹ��ʼ����ͬ����ͬʱ��ʼ��ֱ���˶������˶���v-tͼ����ͼ��ʾ����A��B�˶�����ķ��������н�����ȷ���ǣ�������| A�� | A��B����ʱ�ļ��ٶȴ�С֮��Ϊ5��1�� | |
| B�� | A��B����ʱ�ļ��ٶȴ�С֮��Ϊ2��1 | |
| C�� | ��t=3t0ʱ�̣�A��B�����Զ | |
| D�� | ��t=6t0ʱ�̣�A��B���� |
 ��ԭ�ӵIJ����ܼ���ͼ��ʾ����֪�ɼ���Ĺ���������1.62eV��3.11eV֮�䣬�ɴ˿���֪����ԭ�ӣ�������
��ԭ�ӵIJ����ܼ���ͼ��ʾ����֪�ɼ���Ĺ���������1.62eV��3.11eV֮�䣬�ɴ˿���֪����ԭ�ӣ�������| A�� | �Ӹ��ܼ���n=1�ܼ�ԾǨʱ�����Ĺ�IJ����ȿɼ���Ķ� | |
| B�� | �Ӹ��ܼ���n=2�ܼ�ԾǨʱ�����Ĺ��Ϊ�ɼ��� | |
| C�� | ��n=3�ܼ���n=2�ܼ�ԾǨʱ�����Ĺ�Ϊ�ɼ��� | |
| D�� | ��n=4�ܼ���n=2�ܼ�ԾǨʱ�����Ĺ�Ϊ�ɼ��� | |
| E�� | �Ӹ��ܼ�n=3�ܼ�ԾǨʱ�����Ĺ��Ƶ�ʱȿɼ���ĸ� |
 �綴ʵ�����ܲ�����С�ͷ�����ɸı�ķ�������ͼ��ʾ���ڷ綴ʵ���������㹻��Ĺ⻬ˮƽ�棬��ˮƽ���Ͻ���xOyֱ������ϵ������m=0.5kg��С���Գ��ٶ�v0=0.40m/s��O����x���������˶�����0��2.0s���ܵ�һ����y��������СF1=0.20N�ķ������ã�С���˶�2.0s����������Ϊy�Ḻ����С��ΪF2=0.10N��ͼ��δ������������
�綴ʵ�����ܲ�����С�ͷ�����ɸı�ķ�������ͼ��ʾ���ڷ綴ʵ���������㹻��Ĺ⻬ˮƽ�棬��ˮƽ���Ͻ���xOyֱ������ϵ������m=0.5kg��С���Գ��ٶ�v0=0.40m/s��O����x���������˶�����0��2.0s���ܵ�һ����y��������СF1=0.20N�ķ������ã�С���˶�2.0s����������Ϊy�Ḻ����С��ΪF2=0.10N��ͼ��δ������������ ��ͼ��һ����Ǧ�=30��Ĺ⻬ֱ��������б���̶���ˮƽ�����ϣ���������һ���ʹ⻬�����֣�����Ϊm��A�������ڵ��棬�϶��뾢��ϵ��Ϊk����ֱ�ᵯ��������һ����������������֣�һ����б��������Ϊm��B������������һ���뵯���϶����ӣ�����ϸ�ߺ�A��B�����λ�ã�ʹ���ɴ���ԭ��״̬����ϸ����Ȼ��ֱ��������б����������ƽ�У��ֽ�B�����ɾ�ֹ�ͷţ���֪B����ǡ����ʹA�����Ҫ�뿪���浫��������������
��ͼ��һ����Ǧ�=30��Ĺ⻬ֱ��������б���̶���ˮƽ�����ϣ���������һ���ʹ⻬�����֣�����Ϊm��A�������ڵ��棬�϶��뾢��ϵ��Ϊk����ֱ�ᵯ��������һ����������������֣�һ����б��������Ϊm��B������������һ���뵯���϶����ӣ�����ϸ�ߺ�A��B�����λ�ã�ʹ���ɴ���ԭ��״̬����ϸ����Ȼ��ֱ��������б����������ƽ�У��ֽ�B�����ɾ�ֹ�ͷţ���֪B����ǡ����ʹA�����Ҫ�뿪���浫�������������� ��ͼ��ʾ����������ʾ�Ŀ��ȷ�Χ�ڣ��õ糡ǿ��ΪE����ǿ�糡��ʹ�Գ��ٶ�v0��ֱ�ڵ糡�����ij������ƫת�Ƚǣ���ͬ���Ŀ��ȷ�Χ�ڣ������÷���ֱ��ֽ���������ǿ�ų���ʹ���Ӵ����ų������ƫ��ҲΪ�ȣ�����ǿ�ų��ĴŸ�Ӧǿ�ȴ�СΪ���٣�
��ͼ��ʾ����������ʾ�Ŀ��ȷ�Χ�ڣ��õ糡ǿ��ΪE����ǿ�糡��ʹ�Գ��ٶ�v0��ֱ�ڵ糡�����ij������ƫת�Ƚǣ���ͬ���Ŀ��ȷ�Χ�ڣ������÷���ֱ��ֽ���������ǿ�ų���ʹ���Ӵ����ų������ƫ��ҲΪ�ȣ�����ǿ�ų��ĴŸ�Ӧǿ�ȴ�СΪ���٣�