题目内容
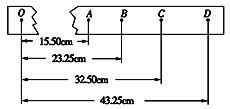
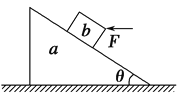
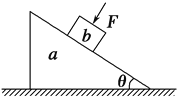
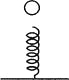
【题目】如图所示,长木板A右边固定着一个挡板,包括挡板在内的总质量为1.5M,静止在光滑的水平地面上.小木块B质量为M,从A的左端开始以初速度v0在A上滑动,滑到右端与挡板发生碰撞,已知碰撞过程时间极短,碰后木块B恰好滑到A的左端就停止滑动.已知B与A间的动摩擦因数为μ,B在A板上单程滑行长度为l.求:

(1)若μl=3v02/160g,在B与挡板碰撞后的运动过程中,摩擦力对木板A做正功还是负功?做多少功?
(2)讨论A和B在整个运动过程中,是否有可能在某一段时间里运动方向是向左的.如果不可能,说明理由;如果可能,求出发生这种情况的条件.
【答案】(1)0.068Mv02(2)2v02/15g<μl≤3v02/20g
【解析】(1)B与A碰撞后,B相对于A向左运动,A所受摩擦力方向向左,A的运动方向向右,故摩擦力作负功.设B与A碰撞后的瞬间A的速度为v1,B的速度为v2,A、B相对静止后的共同速度为v,整个过程中A、B组成的系统动量守恒,有
Mv0=(M+1.5M)v
解得:v=2v0/5.
碰撞后直至相对静止的过程中,系统动量守恒,机械能的减少量等于系统克服摩擦力做的功,即Mv2+1.5Mv1=2.5Mv①
![]() ×1.5Mv12+
×1.5Mv12+![]() Mv22-
Mv22-![]() ×2.5Mv2=Mμlg,②
×2.5Mv2=Mμlg,②
可解出v1=![]() v0(另一解v1=
v0(另一解v1=![]() v0因小于v而舍去)
v0因小于v而舍去)
这段过程中,A克服摩擦力做功
W=![]() ×1.5Mv12-
×1.5Mv12-![]() ×1.5Mv2=
×1.5Mv2=![]() Mv02(0.068Mv02).
Mv02(0.068Mv02).
(2)A在运动过程中不可能向左运动,因为在B未与A碰撞之前,A受到的摩擦力方向向右,做加速运动,碰撞之后A受到的摩擦力方向向左,做减速运动,直到最后,速度仍向右,因此不可能向左运动.
B在碰撞之后,有可能向左运动,即v2<0.先计算当v2=0时满足的条件,由①式,得
v1=(2v0/3)-(2v2/3),
当v2=0时,v1=2v0/3,代入②式,
得(![]() ×1.5M×
×1.5M×![]() )-(
)-(![]() ×2.5M×
×2.5M×![]() )=Mμgl
)=Mμgl
解得μlg=![]()
B在某段时间内向左运动的条件之一是μl<![]()
另一方面,整个过程中损失的机械能一定大于或等于系统克服摩擦力做的功,即
![]() Mv02-
Mv02-![]() 2.5M(
2.5M(![]() )2≥2Mμlg,
)2≥2Mμlg,
解出另一个条件是![]()
最后得出B在某段时间内向左运动的条件是![]() .
.

 发散思维新课堂系列答案
发散思维新课堂系列答案