题目内容
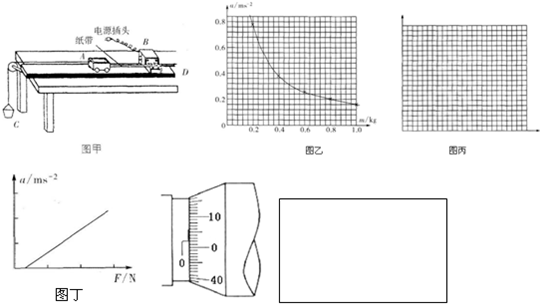
(1)图l为“探究加速度与力、质量的关系”实验装置图.图中A为小车,B为砝码及砝码盘,C为一端带有定滑轮的长木板,小车通过纸带与电火花打点计时器相连,计时器接50Hz交流电.小车A的质量为m1,砝码及砝码盘B的质量为m2.
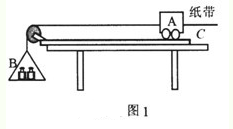
①下列说法正确的是
A.每次改变小车质量时,应重新平衡摩擦力
B.实验时应先释放小车后接通电源
C.本实验m2应远小于m1
D.在用图象探究加速度与质量关系时,应作a-
图象
②实验时,某同学由于疏忽,遗漏了平衡摩擦力这一步骤,他测量得到的a-F图象,可能是图2中的
③图3为某次实验得到的纸带,纸带中相邻计数点间的距离已标出,相邻计数点间还有四个点没有画出.由此可求得小车的加速度大小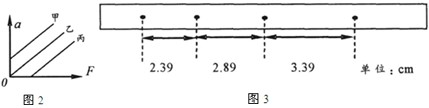
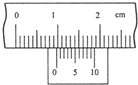
(2)①某实验小组在“测定金属电阻率”的实验过程中,正确操作获得金属丝的直径以及电流表、电压表的读数如第34题图4所示,则它们的读数值依次是
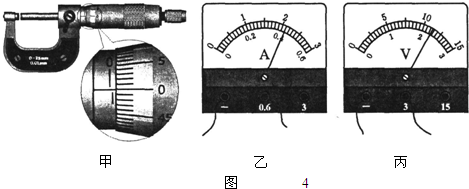
②已知实验中所用的电流表内阻约几欧,电压表内阻约20kΩ,则本实验电路应当采用第34题图5中的
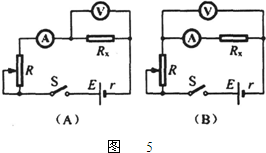
③若已知实验所用的电流表内阻的准确值为RA=2.0Ω,那么能准确测量金属丝电阻Rx的电路应选上图中的
-2
-2(用题中字母代号表示).若用米尺测得金属丝的长度为L,用螺旋测微器测得金属丝直径为d,则该金属丝的电阻率ρ=
(用π、d、L、Rx表示).

①下列说法正确的是
A.每次改变小车质量时,应重新平衡摩擦力
B.实验时应先释放小车后接通电源
C.本实验m2应远小于m1
D.在用图象探究加速度与质量关系时,应作a-
| 1 |
| m1 |
②实验时,某同学由于疏忽,遗漏了平衡摩擦力这一步骤,他测量得到的a-F图象,可能是图2中的
丙
丙
(选填“甲”、“乙”、“丙”)③图3为某次实验得到的纸带,纸带中相邻计数点间的距离已标出,相邻计数点间还有四个点没有画出.由此可求得小车的加速度大小
0.50
0.50
m/s2.(结果保留二位有效数字)
(2)①某实验小组在“测定金属电阻率”的实验过程中,正确操作获得金属丝的直径以及电流表、电压表的读数如第34题图4所示,则它们的读数值依次是
0.999
0.999
mm、0.42
0.42
A、2.25
2.25
V.
②已知实验中所用的电流表内阻约几欧,电压表内阻约20kΩ,则本实验电路应当采用第34题图5中的
A
A
(填A或B),用此电路测量的金属丝电阻比真实值偏小
小
(选填“大”或“小”).
③若已知实验所用的电流表内阻的准确值为RA=2.0Ω,那么能准确测量金属丝电阻Rx的电路应选上图中的
B
B
电路(填A或B).若此时测得电流为I、电压为U,则金属丝电阻Rx=| U |
| I |
| U |
| I |
| πd2RX |
| 4L |
| πd2RX |
| 4L |
分析:(1)①实验时应平衡摩擦力,实验时应先接通电源,然后再释放小车;当砝码与砝码盘的质量远小于小车质量时,可以近似认为小车受到的拉力等于砝码与砝码盘的质量;根据牛顿第二定律分析答题.
②实验时应平衡摩擦力,如果不平衡摩擦力,小车受到的合力小于绳的拉力,a-F图象在F轴上有截距.
③小车做的是匀加速直线运动,可由△x=at2求解加速度.
(2)①螺旋测微器固定刻度与可动刻度示数之和是螺旋测微器的示数;先确定电表量程与分度值,然后读出电表示数.
②根据欧姆定律求出金属丝电阻,根据金属丝电阻与电表内阻间的关系确定电流表的接法,然后选择实验电路.
③在已知电流表内阻的情况下,可以采用电流表内接法,由串联电路特点及欧姆定律可以求出待测电阻阻值.
②实验时应平衡摩擦力,如果不平衡摩擦力,小车受到的合力小于绳的拉力,a-F图象在F轴上有截距.
③小车做的是匀加速直线运动,可由△x=at2求解加速度.
(2)①螺旋测微器固定刻度与可动刻度示数之和是螺旋测微器的示数;先确定电表量程与分度值,然后读出电表示数.
②根据欧姆定律求出金属丝电阻,根据金属丝电阻与电表内阻间的关系确定电流表的接法,然后选择实验电路.
③在已知电流表内阻的情况下,可以采用电流表内接法,由串联电路特点及欧姆定律可以求出待测电阻阻值.
解答:解:(1)①A、假设木板倾角为θ,平衡摩擦力后f=mgsinθ=μmgcosθ,sinθ=μcosθ,由此可见,平衡摩擦力取决于斜面的倾角,与物体质量无关,每次改变小车质量时,不需要重新平衡摩擦力,故A错误;
B、实验时应先接通电源后释放小车,故B错误;
C、只有当砝码及砝码盘的m2应远小于小车质量m1时,可以近似认为小车受到的拉力等于砝码及砝码盘的重力,故C正确;
D、由牛顿第二定律F=m1a,得a=
,则a与
成正比,在用图象探究加速度与质量关系时,应作a-
图象,故D正确;故选CD.
②实验时没有平衡摩擦力,a-F图象在F轴上有截距,由图2所示图象可知,图象应该是丙.
③计数点间的时间间隔t=0.02s×5=0.1s,由△x=aT2得:a=
=
=0.50m/s2;
(2)①由图甲所示可知,螺旋测微器固定刻度示数是0.5mm,可动刻度示数是49.9×0.01mm=0.499mm,则螺旋测微器示数为0.5mm+0.499mm=0.999mm;由图乙所示电流表可知,电流表量程是0~0.6A,分度值是0.02A,示数为0.42A;电压表量程是0~3V,分度值是0.1V,示数为2.25V;
②待测电阻阻值R=
=
≈5.4Ω,电流表内阻约几欧,电压表内阻约20kΩ,相对来说电压表内阻远大于待测电阻值阻值,电流表应采用外接法,应选A所示实验电路;由于电压表的分流作用,所测电流偏大,由欧姆定律可知,待测电阻测量值小于真实值.
③已知实验所用的电流表内阻的准确值RA=2.0Ω,那么测量金属丝电阻Rx的最佳电路应是图中的B电路;由欧姆定律可得:RA+RX=
,RX=
-2;电阻RX=ρ
=ρ
,则ρ=
.
故答案为:(1)①CD;②丙;③0.50;(2)①0.999;0.42;2.25;②A;小;③B;
-2;
.
B、实验时应先接通电源后释放小车,故B错误;
C、只有当砝码及砝码盘的m2应远小于小车质量m1时,可以近似认为小车受到的拉力等于砝码及砝码盘的重力,故C正确;
D、由牛顿第二定律F=m1a,得a=
| F |
| m1 |
| 1 |
| m1 |
| 1 |
| m1 |
②实验时没有平衡摩擦力,a-F图象在F轴上有截距,由图2所示图象可知,图象应该是丙.
③计数点间的时间间隔t=0.02s×5=0.1s,由△x=aT2得:a=
| x3-x1 |
| 2t2 |
| 0.0339-0.0239 |
| 2×0.12 |
(2)①由图甲所示可知,螺旋测微器固定刻度示数是0.5mm,可动刻度示数是49.9×0.01mm=0.499mm,则螺旋测微器示数为0.5mm+0.499mm=0.999mm;由图乙所示电流表可知,电流表量程是0~0.6A,分度值是0.02A,示数为0.42A;电压表量程是0~3V,分度值是0.1V,示数为2.25V;
②待测电阻阻值R=
| U |
| I |
| 2.25V |
| 0.42A |
③已知实验所用的电流表内阻的准确值RA=2.0Ω,那么测量金属丝电阻Rx的最佳电路应是图中的B电路;由欧姆定律可得:RA+RX=
| U |
| I |
| U |
| I |
| L |
| S |
| L | ||
π(
|
| πd2RX |
| 4L |
故答案为:(1)①CD;②丙;③0.50;(2)①0.999;0.42;2.25;②A;小;③B;
| U |
| I |
| πd2RX |
| 4L |
点评:(1)会根据实验原理分析分析为什么要平衡摩擦力和让小车的质量M远远大于小桶(及砝码)的质量m,且会根据原理分析实验误差.纸带的处理在高中实验中用到多次,需要牢固的掌握.
(2)螺旋测微器固定刻度与可动刻度所示之和是螺旋测微器的示数,螺旋测微器需要估读;对电流表与电压表读数时,要先确定电表的量程与分度值,然后读数,读数时视线要与电表刻度线垂直.
(2)螺旋测微器固定刻度与可动刻度所示之和是螺旋测微器的示数,螺旋测微器需要估读;对电流表与电压表读数时,要先确定电表的量程与分度值,然后读数,读数时视线要与电表刻度线垂直.

练习册系列答案
相关题目


 (2011?福建)(1)某实验小组在利用单摆测定当地重力加速度的实验中:
(2011?福建)(1)某实验小组在利用单摆测定当地重力加速度的实验中: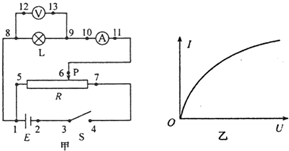




 ⑴(6分)某实验小组在利用单摆测定当地重力加速度的试验中:
⑴(6分)某实验小组在利用单摆测定当地重力加速度的试验中: ①在小电珠接入电路前,使用多用电表直接测量小电珠的电阻,则应将选择开关旋至____档进行测量。(填选项前的字母)
①在小电珠接入电路前,使用多用电表直接测量小电珠的电阻,则应将选择开关旋至____档进行测量。(填选项前的字母) Ⅱ.在实验过程中,已知各元器件均无故障,但闭和开关S后,无论如何调节滑片P,电压表和电流表的示数总是调不到零,其原因是_____点至_____点的导线没有连接好;(图甲中的黑色小圆点表示接线点,并用数字标记,空格中请填写图甲中的数字,如“2点至3点”的导线)
Ⅱ.在实验过程中,已知各元器件均无故障,但闭和开关S后,无论如何调节滑片P,电压表和电流表的示数总是调不到零,其原因是_____点至_____点的导线没有连接好;(图甲中的黑色小圆点表示接线点,并用数字标记,空格中请填写图甲中的数字,如“2点至3点”的导线)