题目内容
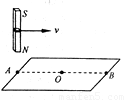
如图,水平桌面上有一轻弹簧,左端固定在A点,自然状态时其右端位于B点.水平桌面右侧有一竖直放置的轨道MNP,其形状为半径R=1.0m的圆环剪去了左上角120°的圆弧,MN为其竖直直径,P点到桌面的竖直距离是h=2.4m.用质量m1=0.4kg的物块将弹簧缓慢压缩到C点,释放后弹簧恢复原长时物块恰停止在B点.用同种材料、质量为m2=0.2kg的物块将弹簧缓慢压缩到C点释放,物块过B点后做匀变速运动其位移与时间的关系为s=6t-2t2,物块飞离桌面后恰好由P点沿切线落入圆轨道.(不计空气阻力,g取10m/s2,sin60°=
,
cos60°=
)求:
(1)物块m2过B点时的瞬时速度vB及与桌面间的滑动摩擦因数μ.
(2)若轨道MNP光滑,小球经过轨道最低点N时对轨道的压力FN.
(3)若小球刚好能到达轨道最高点M,则释放后m2运动过程中克服摩擦力做的功W.
| ||
| 2 |
cos60°=
| 1 |
| 2 |
(1)物块m2过B点时的瞬时速度vB及与桌面间的滑动摩擦因数μ.
(2)若轨道MNP光滑,小球经过轨道最低点N时对轨道的压力FN.
(3)若小球刚好能到达轨道最高点M,则释放后m2运动过程中克服摩擦力做的功W.

分析:(1)根据物块的位移公式可以求出物块的速度与加速度,由牛顿第二定律可以求出动摩擦因数.
(2)小球离开桌面后做平抛运动,由平抛运动求出小球离开时的速度,然后由动能定理或机械能守恒定律求出到达N点的速度,再由牛顿第二定律求出在N点小球受到的支持力,由牛顿第三定律求出对轨道的压力.
(3)由牛顿第二定律求出小球在M点的速度,然后由动能定理求出各段克服摩擦力做功,最后求出整个过程克服摩擦力做功.
(2)小球离开桌面后做平抛运动,由平抛运动求出小球离开时的速度,然后由动能定理或机械能守恒定律求出到达N点的速度,再由牛顿第二定律求出在N点小球受到的支持力,由牛顿第三定律求出对轨道的压力.
(3)由牛顿第二定律求出小球在M点的速度,然后由动能定理求出各段克服摩擦力做功,最后求出整个过程克服摩擦力做功.
解答:解:(1)m2过B点后遵从:s=6t-2t2,
由此可知,vB=6m/s,a=-4m/s2.
由牛顿第二定律得:μmg=ma,解得:μ=0.4;
(2)小球离开桌面后做平抛运动,
在竖直方向上:h=
=2.4m,
P点速度在竖直方向的分量:
vy=vDtan60°=4
m/s,
解得离开D点的速度为vD=4m/s,
由机械能守恒定律得:
mvN2=
mvD2+mg(h+R-Rcosθ),
解得:vN2=74m2/s2,
在N点,由牛顿第二定律得:
FN′-mg=m
,解得:FN′=42N,
由牛顿第三定律得,压力:F=F'=42N,方向竖直向下.
(3)小球刚好能到达M点,
由牛顿第二定律得:mg=m
,
小球到达P点的速度vP=
=8m/s.
从P到M点,由动能定理得:
-mgR(1+cosθ)-WPM=
mvM2+-
mvP2,解得:WPM=2.4J;
从B到D点,由动能定理得:-WBD=
mvD2-
mvB2,解得:WBD=2J;
从C到B点,由动能定理得:EP=μm1gxCB,EP=μm2gxCB+
m2vB2,
解得:3μm2gxCB=
m2vB2,WCB=3μm2gxCB=1.2J,
则释放后m2运动过程中克服摩擦力做的功为:
W=WCB+WBD+WPM=1.2J+2J+2.4J=5.6J;
答:(1)物块m2过B点时的瞬时速度vB为6m/s,与桌面间的滑动摩擦因数为0.4.
(2)若轨道MNP光滑,小球经过轨道最低点N时对轨道的压力为42N方向竖直向下.
(3)若小球刚好能到达轨道最高点M,则释放后m2运动过程中克服摩擦力做的功为5.6J.
由此可知,vB=6m/s,a=-4m/s2.
由牛顿第二定律得:μmg=ma,解得:μ=0.4;
(2)小球离开桌面后做平抛运动,
在竖直方向上:h=
| ||
| 2g |
P点速度在竖直方向的分量:
vy=vDtan60°=4
| 3 |
解得离开D点的速度为vD=4m/s,
由机械能守恒定律得:
| 1 |
| 2 |
| 1 |
| 2 |
解得:vN2=74m2/s2,
在N点,由牛顿第二定律得:
FN′-mg=m
| ||
| R |
由牛顿第三定律得,压力:F=F'=42N,方向竖直向下.
(3)小球刚好能到达M点,
由牛顿第二定律得:mg=m
| ||
| R |
小球到达P点的速度vP=
|
从P到M点,由动能定理得:
-mgR(1+cosθ)-WPM=
| 1 |
| 2 |
| 1 |
| 2 |
从B到D点,由动能定理得:-WBD=
| 1 |
| 2 |
| 1 |
| 2 |
从C到B点,由动能定理得:EP=μm1gxCB,EP=μm2gxCB+
| 1 |
| 2 |
解得:3μm2gxCB=
| 1 |
| 2 |
则释放后m2运动过程中克服摩擦力做的功为:
W=WCB+WBD+WPM=1.2J+2J+2.4J=5.6J;
答:(1)物块m2过B点时的瞬时速度vB为6m/s,与桌面间的滑动摩擦因数为0.4.
(2)若轨道MNP光滑,小球经过轨道最低点N时对轨道的压力为42N方向竖直向下.
(3)若小球刚好能到达轨道最高点M,则释放后m2运动过程中克服摩擦力做的功为5.6J.
点评:该题涉及到多个运动过程,主要考查了机械能守恒定律、平抛运动基本公式、圆周运动向心力公式的应用,用到的知识点及公式较多,难度较大,属于难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
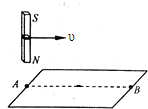 如图所示桌面上有一铜制矩形线框,AB是线框的中轴线.一条形磁铁以速度υ水平向右匀速通过AB正上方,整个过程中线框始终静止.条形磁铁经过A点和B点正上方时,对线框的受力情况判断正确的是( )
如图所示桌面上有一铜制矩形线框,AB是线框的中轴线.一条形磁铁以速度υ水平向右匀速通过AB正上方,整个过程中线框始终静止.条形磁铁经过A点和B点正上方时,对线框的受力情况判断正确的是( ) 如图所示桌面上有一铜制矩形线框,AB是线框的中轴线,O为AB的中点.一条形磁铁水平匀速通过AB正上方的过程中,线框始终静止.则下列说法中正确的是( )
如图所示桌面上有一铜制矩形线框,AB是线框的中轴线,O为AB的中点.一条形磁铁水平匀速通过AB正上方的过程中,线框始终静止.则下列说法中正确的是( )