题目内容
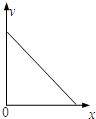
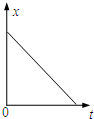
如图所示,一水平放置的圆盘绕竖直固定轴转动,在圆盘上沿半径开有一条宽度为2 mm的均匀狭缝.将激光器与传感器上下对准,使二者间连线与转轴平行,分别置于圆盘的上下两侧.开始时,激光器和传感器在转轴位置,并由静止起同步地沿圆盘半径方向做匀加速移动,激光器连续向下发射激光束.在圆盘转动过程中,当狭缝经过激光器与传感器之间时,传感器接收到一个激光信号,并将其输入计算机,经处理后画出相应图线.图甲为该装置示意图,图乙为所接收的光信号随时间变化的图线,横坐标表示时间,纵坐标表示接收到的激光信号强度,图中Δt1=8.0×10-3 s,Δt2=2.0×10-3 s.
图甲

图乙
(1)利用图乙中的数据求1.6 s时圆盘转动的角速度;
(2)试求出激光器和传感器沿半径向外移动的加速度大小;
(3)求图乙中第三个激光信号的宽度Δt3.
解答:(1)由图线读得,转盘的转动周期T=0.8 s①
角速度ω=![]() rad/s=7.85 rad/s.②
rad/s=7.85 rad/s.②
(2)激光器和探测器沿半径由中心向边缘移动时的加速度为a,经过一个周期后,它们离开圆心的距离为
r1=![]() aT2③
aT2③
该半径处转盘的线速度为:
v1=ωr1④
转动一周后,传感器接收到一个激光信号的时间间隔为:
Δt1=![]() T⑤
T⑤
由上述三式可以求得a=![]() =0.10 m/s2.
=0.10 m/s2.
(3)设狭缝宽度为d,探测器接收到第i个脉冲时距转轴的距离为ri,第i个脉冲的宽度为Δti,激光器和探测器沿半径的运动速度为v.
Δt1=![]() T⑥
T⑥
r3=![]() a(3T)2=9r1⑦
a(3T)2=9r1⑦
由⑤⑥⑦式解得:
Δt3=![]() Δt1=8.9×10-4 s.
Δt1=8.9×10-4 s.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,一水平放置的平行板电容器,上下极板间存在匀强电场,其间有一带电小球从A点以某一初速度沿虚线AB运动,则在小球从A运动到B的过程中( )
如图所示,一水平放置的平行板电容器,上下极板间存在匀强电场,其间有一带电小球从A点以某一初速度沿虚线AB运动,则在小球从A运动到B的过程中( ) 如图所示,一水平放置的平行板电容器充完电后一直与电源相连,带正电的极板接地,两极板间在P点固定一带正电的点电荷,若将负极板向下移动一小段距离稳定后(两板仍正对平行),则下列说法中正确的是( )
如图所示,一水平放置的平行板电容器充完电后一直与电源相连,带正电的极板接地,两极板间在P点固定一带正电的点电荷,若将负极板向下移动一小段距离稳定后(两板仍正对平行),则下列说法中正确的是( ) 如图所示,一水平放置的平行板电容器充完电后一直与电源相连,带正电的极板接地,两极板间在P点固定一带正电的点电荷,若将负极板向下移动一小段距离稳定后(两板仍正对平行),则下列说法中正确的是( )
如图所示,一水平放置的平行板电容器充完电后一直与电源相连,带正电的极板接地,两极板间在P点固定一带正电的点电荷,若将负极板向下移动一小段距离稳定后(两板仍正对平行),则下列说法中正确的是( )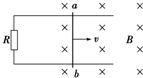 如图所示,一水平放置的平行导体框架宽度L=0.50m,接有电阻R=0.20Ω,磁感应强度B=0.40T的匀强磁场垂直导轨平面方向向下,仅有一导体棒ab跨放在框架上,并能无摩擦地沿框架滑动,框架及导体棒ab电阻不计,当ab以v=4.0m/s的速度向右匀速滑动时.试求:
如图所示,一水平放置的平行导体框架宽度L=0.50m,接有电阻R=0.20Ω,磁感应强度B=0.40T的匀强磁场垂直导轨平面方向向下,仅有一导体棒ab跨放在框架上,并能无摩擦地沿框架滑动,框架及导体棒ab电阻不计,当ab以v=4.0m/s的速度向右匀速滑动时.试求: 如图所示,一水平放置的光滑平行导轨上放一质量为m的金属杆,导轨间距为L,导轨的一端连接一阻值为R的电阻,金属杆与导轨的电阻不计,磁感应强度为B的匀强磁场垂直于导轨平面.现给金属杆一个水平向右的初速度v0,让其自由滑行,导轨足够长,则金属杆滑行过程所受安培力F、运动速度v、加速度a、位移x大致图象正确的是( )
如图所示,一水平放置的光滑平行导轨上放一质量为m的金属杆,导轨间距为L,导轨的一端连接一阻值为R的电阻,金属杆与导轨的电阻不计,磁感应强度为B的匀强磁场垂直于导轨平面.现给金属杆一个水平向右的初速度v0,让其自由滑行,导轨足够长,则金属杆滑行过程所受安培力F、运动速度v、加速度a、位移x大致图象正确的是( )