题目内容
20. 在粗糙的水平面上有两个静止的物体A、B,它们的质量均为(a).A与水平面间的动摩擦因数为μ1=0.4,B与水平面间的动摩擦因数μ2=0.2.在水平恒力F=20N的作用下从静止开始向右做匀加速直线运动,F作用了t=2s然后撤掉.
在粗糙的水平面上有两个静止的物体A、B,它们的质量均为(a).A与水平面间的动摩擦因数为μ1=0.4,B与水平面间的动摩擦因数μ2=0.2.在水平恒力F=20N的作用下从静止开始向右做匀加速直线运动,F作用了t=2s然后撤掉.求:A、B都静止时它们之间的距离L.(g=10m/s2)
分析 对整体受力分析及牛顿第二定律可求得整体的加速度,由运动学公式可求得2s时的速度;
再由牛顿第二定律可求得撤去拉力后的加速度,由运动学公式可求得二者静止时的距离,从而求出二者间的距离.
解答 解:由牛顿第二定律得:
F-μ1mg-μ2mg=2ma
得:a=$\frac{F-{μ}_{1}mg-{μ}_{2}mg}{2m}$$\frac{20-0.4×2×10-0.2×2×10}{2×2}$=2m/s2
2s末的速度为:v=at=2×2=4m/s
撤去力F后:
A的加速度大小为:aA=μ1g=0.4×10=4m/s2;
A的位移大小为:xA=$\frac{{v}^{2}}{2{a}_{A}}$=$\frac{{4}^{2}}{2×4}$=2m;
B的加速度大小为:aB=μ2g=2m/s2;
B的位移大小为:xB=$\frac{{v}^{2}}{2{a}_{B}}$=$\frac{{4}^{2}}{2×2}$=4m;
所以A、B都静止时它们之间的距离为:L=xB-xA=2m
答:A、B都静止时它们之间的距离L为2m.
点评 本题考查牛顿第二定律及运动学公式的应用,要注意正确进行受力分析及运动学过程分析.

练习册系列答案
相关题目
11. 某同学按图所示电路连接实物,闭合开关后,发现灯泡不亮.他将高内阻的电压表并联在A、C之间时,电压表的读数为U,当并联在A、B之间时,电压表的读数也为U,当并联在B、C之间时,电压表的读数为0,则故障可能是( )
某同学按图所示电路连接实物,闭合开关后,发现灯泡不亮.他将高内阻的电压表并联在A、C之间时,电压表的读数为U,当并联在A、B之间时,电压表的读数也为U,当并联在B、C之间时,电压表的读数为0,则故障可能是( )
 某同学按图所示电路连接实物,闭合开关后,发现灯泡不亮.他将高内阻的电压表并联在A、C之间时,电压表的读数为U,当并联在A、B之间时,电压表的读数也为U,当并联在B、C之间时,电压表的读数为0,则故障可能是( )
某同学按图所示电路连接实物,闭合开关后,发现灯泡不亮.他将高内阻的电压表并联在A、C之间时,电压表的读数为U,当并联在A、B之间时,电压表的读数也为U,当并联在B、C之间时,电压表的读数为0,则故障可能是( )| A. | AB段断路 | B. | BC段断路 | C. | AB段短路 | D. | 无法判定 |
8.下列说法正确的是( )
| A. | 一对相互作用力的合力为零 | |
| B. | 物体只有重心处受到重力的作用 | |
| C. | 物体在一恒力作用下可能做曲线运动 | |
| D. | 力是矢量,位移是矢量,所以功也是矢量 |
15.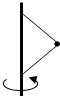 如图,用两根长度均为L的轻绳将一个小球系在竖直转轴上,两绳张紧后与转轴围成等边三角形.现使小球绕轴做匀速圆周运动.( )
如图,用两根长度均为L的轻绳将一个小球系在竖直转轴上,两绳张紧后与转轴围成等边三角形.现使小球绕轴做匀速圆周运动.( )
 如图,用两根长度均为L的轻绳将一个小球系在竖直转轴上,两绳张紧后与转轴围成等边三角形.现使小球绕轴做匀速圆周运动.( )
如图,用两根长度均为L的轻绳将一个小球系在竖直转轴上,两绳张紧后与转轴围成等边三角形.现使小球绕轴做匀速圆周运动.( )| A. | 小球的角速度大于$\sqrt{\frac{2g}{L}}$时,两绳才会都张紧 | |
| B. | 两绳都张紧时,增大小球的角速度,两绳的张力都会增大 | |
| C. | 两绳都张紧时,增大小球的角速度,两绳的张力的大小之差会增大 | |
| D. | 小球的向心力是两绳对小球的拉力的合力 |
5.下列说法正确的是( )
| A. | 做曲线运动的物体一定有加速度 | |
| B. | 当物体受到的合外力为零时,物体仍可以做曲线运动 | |
| C. | 平抛运动是匀变速运动,任意相等时间内速度的变化都相同 | |
| D. | 匀速圆周运动虽然不是匀变速运动,但任意相等时间内速度的变化仍相同 |
12.从某高处释放一粒小石子甲,经过2s从同一地点释放另一小石子乙,不计空气阻力,则它们落地之前( )
| A. | 两石子之间的距离不断变大 | B. | 两石子之间的距离保持不变 | ||
| C. | 甲相对乙做匀速直线运动 | D. | 甲相对乙做匀加速直线运动 |
9.一质点在某段时间内作曲线运动,则在这段时间内( )
| A. | 速度一定在不断地变化 | B. | 速度可能保持不变 | ||
| C. | 加速度一定不断地变化 | D. | 所受合力一定不断地变化 |
 如图所示,在水平地面上固定一倾角θ=53°、表面光滑的斜面体,物体A以v1=8m/s的初速度沿斜面上滑,同时在物体A的正上方,有一物体B以某一初速度水平抛出.如果当A上滑到最高点时恰好被B物体击中.(A、B均可看作质点,sin53°=0.8,cos53°=0.6,g取10m/s2)求:
如图所示,在水平地面上固定一倾角θ=53°、表面光滑的斜面体,物体A以v1=8m/s的初速度沿斜面上滑,同时在物体A的正上方,有一物体B以某一初速度水平抛出.如果当A上滑到最高点时恰好被B物体击中.(A、B均可看作质点,sin53°=0.8,cos53°=0.6,g取10m/s2)求: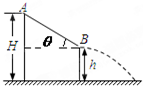 如图所示,一位质量m=60kg的队员在参加一次消防逃生演练中,从倾角为θ=37°直滑道AB的顶端A由静止滑下,经B点后水平滑出,最后落在水平地面的护垫上(不计护垫厚度的影响).已知A、B离水平地面的高度分别为H=6.2m、h=3.2m,队员与滑道间的动摩擦因数μ=0.3,g取10m/s2.求
如图所示,一位质量m=60kg的队员在参加一次消防逃生演练中,从倾角为θ=37°直滑道AB的顶端A由静止滑下,经B点后水平滑出,最后落在水平地面的护垫上(不计护垫厚度的影响).已知A、B离水平地面的高度分别为H=6.2m、h=3.2m,队员与滑道间的动摩擦因数μ=0.3,g取10m/s2.求