题目内容
8.在火车站站台上有一观察者,在列车开动时恰好站在第一节车厢的最前端,列车起动后做匀加速直线运动.3秒末时第一节车厢末端通过观察者(每节车厢等长),则从开始观察经过9s时间第9节车厢的末端通过观察者;第9节车厢通过观察者的时间为$9-6\sqrt{2}$s.分析 根据匀变速直线运动的位移时间公式求出第9节车厢的末端经过观察者的时间.根据初速度为零的匀变速直线运动,在通过相等位移内的时间之比等于1:$(\sqrt{2}-1):(\sqrt{3}-\sqrt{2}):$…($\sqrt{n}-\sqrt{n-1}$)求出第9节车厢通过观察者的时间.
解答 解:根据L=$\frac{1}{2}a{{t}_{1}}^{2}$,9L=$\frac{1}{2}a{{t}_{2}}^{2}$,可知t2=3t1=9s.
初速度为零的匀变速直线运动,在通过相等位移内的时间之比等于1:$(\sqrt{2}-1):(\sqrt{3}-\sqrt{2}):$…($\sqrt{n}-\sqrt{n-1}$),则第一节车厢通过观察者的时间和第9节车厢通过观察者的时间之比为$1:(3-2\sqrt{2})$,可知第9节车厢通过观察者的时间为($9-6\sqrt{2}$)s.
故答案为:9、$9-6\sqrt{2}$
点评 解决本题的关键掌握匀变速直线运动的运动学公式和推论,并能灵活运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.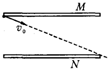 如图所示,水平放置的平行板电容器两极板间距为d,带负电的微粒质量为m、带电量为q,它从上极板的边缘以初速度v0射入,沿直线从下极板N的边缘射出,则( )
如图所示,水平放置的平行板电容器两极板间距为d,带负电的微粒质量为m、带电量为q,它从上极板的边缘以初速度v0射入,沿直线从下极板N的边缘射出,则( )
 如图所示,水平放置的平行板电容器两极板间距为d,带负电的微粒质量为m、带电量为q,它从上极板的边缘以初速度v0射入,沿直线从下极板N的边缘射出,则( )
如图所示,水平放置的平行板电容器两极板间距为d,带负电的微粒质量为m、带电量为q,它从上极板的边缘以初速度v0射入,沿直线从下极板N的边缘射出,则( )| A. | 微粒的加速度不为零 | B. | 微粒的电势能减少了mgd | ||
| C. | 两极板的电势差为$\frac{mgd}{q}$ | D. | M板的电势低于N板的电势 |
17.一个物体沿一条直线运动,其位移s随时间t变化规律图线为如图所示抛物线,c和d已知,由此可知( )


| A. | 物体的初速度为0 | B. | 物体做加速度越来越大的加速运动 | ||
| C. | 物体在c时刻的速度为$\frac{3d}{2c}$ | D. | 物体经过1.5c时的速度为$\frac{d}{c}$ |
 在“探究求合力的方法”的实验中,需要将橡皮条的一端固定在水平木板上,另一端系上两根细绳,细绳的另一端都有绳套(如图).实验中需用两个弹簧秤分别勾住绳套,并互成角度地拉橡皮条,使橡皮条伸长,结点到达某一位置O.
在“探究求合力的方法”的实验中,需要将橡皮条的一端固定在水平木板上,另一端系上两根细绳,细绳的另一端都有绳套(如图).实验中需用两个弹簧秤分别勾住绳套,并互成角度地拉橡皮条,使橡皮条伸长,结点到达某一位置O.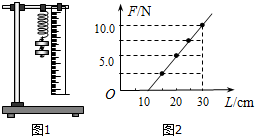 做“探索弹力与弹簧伸长量关系”的实验步骤如下:
做“探索弹力与弹簧伸长量关系”的实验步骤如下:
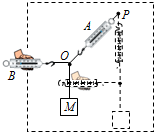 某同学用如图所示的实验装置验证“力的平行四边形定则”.将弹簧测力计A挂于固定点P,下端用细线挂一重物M.弹簧测力计B的挂钩处系一细线,把细线的另一端系在弹簧测力计A下端细线上的O点处,手持弹簧测力计B水平向左拉,使重物静止在如图所示的位置.若已知重物所受的重力为G,弹簧测力计A的拉力方向与竖直方向的夹角为θ,且两弹簧测力计的拉力均不超出它们的量程,则两弹簧测力计的拉力分别为FA=$\frac{G}{cosθ}$,FB=Gtanθ.
某同学用如图所示的实验装置验证“力的平行四边形定则”.将弹簧测力计A挂于固定点P,下端用细线挂一重物M.弹簧测力计B的挂钩处系一细线,把细线的另一端系在弹簧测力计A下端细线上的O点处,手持弹簧测力计B水平向左拉,使重物静止在如图所示的位置.若已知重物所受的重力为G,弹簧测力计A的拉力方向与竖直方向的夹角为θ,且两弹簧测力计的拉力均不超出它们的量程,则两弹簧测力计的拉力分别为FA=$\frac{G}{cosθ}$,FB=Gtanθ.