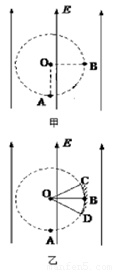
��Ŀ����
 ��ͼ����ʾ����ǿ��СΪE��������ֱ���ϵ���ǿ�糡�ڴ�����һ�뾶ΪR��Բ������O��Ϊ��Բ�������Բ�ģ�A����Բ���������͵㣬B�������Ҳ�ĵ㣮��A���з���Դ�ͷų����ٶȴ�С��ͬ���������ֱ�ڳ�ǿ���ҵ�����ɣ���ɵ�����Ϊm������Ϊq����������������
��ͼ����ʾ����ǿ��СΪE��������ֱ���ϵ���ǿ�糡�ڴ�����һ�뾶ΪR��Բ������O��Ϊ��Բ�������Բ�ģ�A����Բ���������͵㣬B�������Ҳ�ĵ㣮��A���з���Դ�ͷų����ٶȴ�С��ͬ���������ֱ�ڳ�ǿ���ҵ�����ɣ���ɵ�����Ϊm������Ϊq������������������1������ڵ糡���˶��ļ��ٶȶ��
��2���˶��켣����B��ĵ����A��ʱ���ٶȶ��
��3��ij��ɵ��˶��Ĺ켣��Բ������ı�Ե����P�㣬��POA=�ȣ���д���õ�ɾ���P��ʱ���ܵı���ʽ��
��4������Բ������ı�Ե��һ������CBD��C��D�ֱ�Ϊ�����������Ե�����㣬��ͼ�ң���COB=��BOD=30�㣮������Ͻ��յ��ĵ�ɵ�ĩ���ܴ�С�ķ�Χ��
��������ɴ�A��P����ƽ���˶�����ţ�ٵڶ�����������ٶȣ����ˮƽ����������ֱ���˶�����ֱ�������ȼ���ֱ���˶����˵��ˮƽλ��ΪRsin�ȣ���ֱλ��ΪR-Rcos�ȣ����˶�ѧ��ʽ�ͼ��ι�ϵ����õ�ɴ�A�����ʱ�����ʣ�
����ɴ�C��ʱ���糡���������ɻ�õĶ��������D��糡����С����õĶ�����С�����ݶ��ܶ����������Ͻ��յ��ĵ�ɵ�����ܺ���С���ܣ�
����ɴ�C��ʱ���糡���������ɻ�õĶ��������D��糡����С����õĶ�����С�����ݶ��ܶ����������Ͻ��յ��ĵ�ɵ�����ܺ���С���ܣ�
����⣺��1������ţ�ٵڶ����ɵã�a=
��
��2����R=v0t��R=
at2 ��a=
�ã�
��������ʽ�ӿɽ�ã�v0=
��
��3��Rsin��=v0t��R-Rcos��=
at2��a=
����ʽ�ӿɵ�v02=
m v02=
=
����P��ʱ�Ķ��ܣ�Ek=Eq��R-Rcos�ȣ�+
m v02=
EqR ��5-3cos�ȣ�
��4���ɵڣ�3��С��Ľ��ۿ��Կ��������ȴ�0��仯��180�㣬�������ϵ�ɵĶ������������D����յ��ĵ�ɵ�ĩ������С��C����յ��ĵ�ɵ�ĩ�������2�֣�
EkD=Eq��R-Rcos�ȣ�+
m v0D2=
EqR ��5-3cos60�㣩=
EqR
EkC=Eq��R-Rcos�ȣ�+
m v0C2=
EqR ��5-3cos120�㣩=
EqR
���ԣ����Ͻ��յ��ĵ�ɵ�ĩ���ܴ�С�ķ�ΧΪ[
EqR��
EqR]
�𣺣�1������ڵ糡���˶��ļ��ٶ�Ϊ
��
��2���˶��켣����B��ĵ����A��ʱ���ٶ�Ϊ
��
��3���õ�ɾ���P��ʱ���ܵı���ʽ
EqR ��5-3cos�ȣ�
��4�������Ͻ��յ��ĵ�ɵ�ĩ���ܴ�С�ķ�ΧΪ[
EqR��
EqR]��
| qE |
| m |
��2����R=v0t��R=
| 1 |
| 2 |
| qE |
| m |
��������ʽ�ӿɽ�ã�v0=
|
��3��Rsin��=v0t��R-Rcos��=
| 1 |
| 2 |
| qE |
| m |
| Rsin2�� |
| 2m(1-cos��) |
| 1 |
| 2 |
| Rsin2�� |
| 4(1-cos��) |
| R(1+cos��) |
| 4 |
����P��ʱ�Ķ��ܣ�Ek=Eq��R-Rcos�ȣ�+
| 1 |
| 2 |
| 1 |
| 4 |
��4���ɵڣ�3��С��Ľ��ۿ��Կ��������ȴ�0��仯��180�㣬�������ϵ�ɵĶ������������D����յ��ĵ�ɵ�ĩ������С��C����յ��ĵ�ɵ�ĩ�������2�֣�
EkD=Eq��R-Rcos�ȣ�+
| 1 |
| 2 |
| 1 |
| 4 |
| 7 |
| 8 |
EkC=Eq��R-Rcos�ȣ�+
| 1 |
| 2 |
| 1 |
| 4 |
| 13 |
| 8 |
���ԣ����Ͻ��յ��ĵ�ɵ�ĩ���ܴ�С�ķ�ΧΪ[
| 7 |
| 8 |
| 13 |
| 8 |
�𣺣�1������ڵ糡���˶��ļ��ٶ�Ϊ
| qE |
| m |
��2���˶��켣����B��ĵ����A��ʱ���ٶ�Ϊ
|
��3���õ�ɾ���P��ʱ���ܵı���ʽ
| 1 |
| 4 |
��4�������Ͻ��յ��ĵ�ɵ�ĩ���ܴ�С�ķ�ΧΪ[
| 7 |
| 8 |
| 13 |
| 8 |
������������ƽ���˶��Ͷ��ܶ������ۺ�Ӧ�ã�ͬʱҪ���Ӧ�ü���֪ʶ������⣮

��ϰ��ϵ�д�
 Сѧ���AB��ϵ�д�
Сѧ���AB��ϵ�д�
�����Ŀ
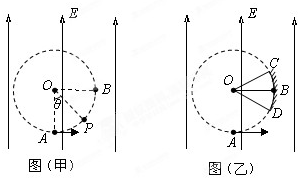 ��ͼ����ʾ����ǿ��СΪE��������ֱ���ϵ���ǿ�糡�ڴ���һ��ֱƽ���ڰ뾶ΪR��Բ������O��Ϊ��Բ�������Բ�ģ�A����Բ���������͵㣬B�������Ҳ�ĵ㣬��A�����Դ�ͷų����ٶȴ�С��ͬ���������ֱ�ڳ�ǿ���ҵ�����ɣ���ɵ�����Ϊm������Ϊq����������������
��ͼ����ʾ����ǿ��СΪE��������ֱ���ϵ���ǿ�糡�ڴ���һ��ֱƽ���ڰ뾶ΪR��Բ������O��Ϊ��Բ�������Բ�ģ�A����Բ���������͵㣬B�������Ҳ�ĵ㣬��A�����Դ�ͷų����ٶȴ�С��ͬ���������ֱ�ڳ�ǿ���ҵ�����ɣ���ɵ�����Ϊm������Ϊq����������������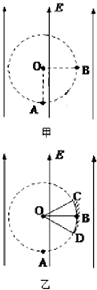 ��ͼ����ʾ����ǿ��СΪE��������ֱ���ϵ���ǿ�糡�ڴ�����һ�뾶ΪR��Բ������O��Ϊ��Բ�������Բ�ģ�A����Բ���������͵㣬B����Բ���������Ҳ�ĵ㣮��A���з���Դ�ͷų����ٶȴ�С��ͬ���������ֱ�ڳ�ǿ���ҵ�����ɣ���ɵ�������Ϊm��������Ϊq����������������
��ͼ����ʾ����ǿ��СΪE��������ֱ���ϵ���ǿ�糡�ڴ�����һ�뾶ΪR��Բ������O��Ϊ��Բ�������Բ�ģ�A����Բ���������͵㣬B����Բ���������Ҳ�ĵ㣮��A���з���Դ�ͷų����ٶȴ�С��ͬ���������ֱ�ڳ�ǿ���ҵ�����ɣ���ɵ�������Ϊm��������Ϊq����������������