题目内容
 如图所示,光滑固定斜面上有一个质量为10kg的小球被轻绳拴住悬挂在天花板上,已知绳子与竖直方向的夹角为45°,斜面倾角30°,整个装置处于静止状态,(g取10m/s2);求:(所有结果均保留三位有效数字)
如图所示,光滑固定斜面上有一个质量为10kg的小球被轻绳拴住悬挂在天花板上,已知绳子与竖直方向的夹角为45°,斜面倾角30°,整个装置处于静止状态,(g取10m/s2);求:(所有结果均保留三位有效数字)
(1)绳中拉力的大小和斜面对小球支持力的大小;
(2)若另外用一个外力拉小球,能够把小球拉离斜面,求最小的拉力的大小.
解:(1)如图,水平竖直建立直角坐标系,对小球做受力分析,把不在轴上的力沿轴分解,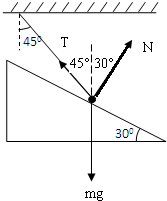
列平衡方程如下 Tcos45°-Nsin30°=0
Tsin45°+Ncos30°-mg=0
由以上两式解得N=73.2N,T=51.8N
(2)当所用的拉力与绳子垂直向右时,经分析得拉力的最小值为Fm=mgsin45°
代数解得Fm=70.7N
答:
(1)绳中拉力的大小和斜面对小球支持力的大小分别为51.8N和73.2N;
(2)若另外用一个外力拉小球,能够把小球拉离斜面,最小的拉力的大小为70.7N.
分析:(1)对小球受力分析,建立直角坐标系,根据平衡条件列方程,求解;
(2)要能够把小球拉离斜面,当所用的拉力与绳子垂直向右时,根据平衡条件求解最小拉力.
点评:解决本题的关键是正确的选取研究对象,进行受力分析,运用正交分解进行求解.

列平衡方程如下 Tcos45°-Nsin30°=0
Tsin45°+Ncos30°-mg=0
由以上两式解得N=73.2N,T=51.8N
(2)当所用的拉力与绳子垂直向右时,经分析得拉力的最小值为Fm=mgsin45°
代数解得Fm=70.7N
答:
(1)绳中拉力的大小和斜面对小球支持力的大小分别为51.8N和73.2N;
(2)若另外用一个外力拉小球,能够把小球拉离斜面,最小的拉力的大小为70.7N.
分析:(1)对小球受力分析,建立直角坐标系,根据平衡条件列方程,求解;
(2)要能够把小球拉离斜面,当所用的拉力与绳子垂直向右时,根据平衡条件求解最小拉力.
点评:解决本题的关键是正确的选取研究对象,进行受力分析,运用正交分解进行求解.

练习册系列答案
相关题目
 (2010?普陀区一模)如图所示,光滑的斜劈放在水平面上,斜面上用固定的竖直板挡住一个光滑球,当整个装置沿水平面以速度v匀速运动时,以下说法中正确的是( )
(2010?普陀区一模)如图所示,光滑的斜劈放在水平面上,斜面上用固定的竖直板挡住一个光滑球,当整个装置沿水平面以速度v匀速运动时,以下说法中正确的是( ) 如图所示,光滑的斜劈放在水平面上,斜面上用固定的竖直板挡住一个光滑球,当整个装置沿水平面方向向右作用匀加速运动时,以下说法中正确的是( )
如图所示,光滑的斜劈放在水平面上,斜面上用固定的竖直板挡住一个光滑球,当整个装置沿水平面方向向右作用匀加速运动时,以下说法中正确的是( )
