题目内容
【题目】一探险队员在探险时遇到一山沟，山沟的一侧OA竖直，另一侧坡面的截面边界OB呈抛物线形状，与一水平平台BC相连 . 如图所示，以沟底的O点为原点建立坐标系Oxy . 已知山沟竖直一侧的高度为2h；抛物线OB的方程为
，平台BC距离沟底高为h，C点离OA的水平距离为2h . 此队员从山沟的竖直一侧，以初速度v0沿水平方向跳向另一侧坡面.探险队员质量为m. 人视为质点，忽略空气阻力，重力加速度为g.求：
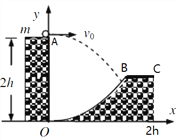
（1）若探险队员以初速度v0水平跳出时，掉在坡面OB的某处，则他在空中运动的时间为多少？
（2）为了能跳在平台上，他的初速度应满足什么条件？请计算说明.
【答案】(1)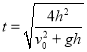 
(2) 
【解析】（1）设探险队员在OB坡面上的落点坐标为（x，y），由平抛规律可得：
x=v0t，
2h-y=
gt2，又
，
以上三式联立可得： 
．
（2）将y=h代入
，可求得：xB=
h．
由平抛规律得：xB=vOBt1，xC=vOCt1，2h-h=
gt12
解得：vOB=
，vOC=
．
所以为了能跳到平台上，他在A点的初速度应满足： 
≤v0≤
．
练习册系列答案
相关题目
