Question

如图，两个固定的倾角相同的滑杆上分别套A、B两个圆环，两个圆环上分别用细线悬吊着两个物体C、D，当它们都沿滑杆向下滑动时，A的悬线始终与杆垂直，B的悬线始终竖直向下。则下列说法中正确的是

1. A.
   A环与滑杆无摩擦力
2. B.
   B环与滑杆无摩擦力
3. C.
   A环做的是匀速运动
4. D.
   B环做的是匀加速运动

Answer 1

A
分别对A、C受力分析，由于两个球加速度相同，故根据牛顿第二定律列式分析可以求出摩擦力；先对D受力分析，结合运动情况判断出D做匀速运动，再对B受力分析．A、C、假设A环与杆间的摩擦力为f，对A环受力分析，受重力、拉力、支持力，假设有向后的摩擦力f，如图，

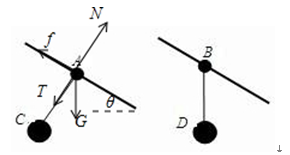
根据牛顿第二定律，有
运动方向：m_Agsinθ-f=m_Aa   ①
对C，同样有
m_Cgsinθ=m_Ca    ②
由①②两式，解得
f=0
a=gsinθ
故A正确，C错误；
B、D、对D球受力分析，受重力和拉力，由于做直线运动，合力与速度在一条直线上，故合力为零，物体做匀速运动；再对B求受力分析，如图，受重力、拉力、支持力，由于做匀速运动，合力为零，故必有向后的摩擦力．

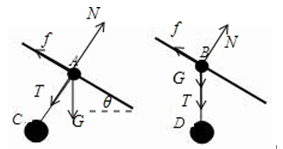
故B错误，D错误；
故选A．
点评：本题关键要结合运动情况判断力，再结合受力情况判断运动情况．