题目内容
【题目】如图所示,一个带圆弧轨道的平台固定在水平地面上,光滑圆弧MN的半径为R=3.2m,水平部分NP长L=3.5m,物体B静止在足够长的平板小车C上,B与小车的接触面光滑,小车的左端紧贴平台的右端。从M点由静止释放的物体A滑至轨道最右端P点后再滑上小车,物体A滑上小车后若与物体B相碰必粘在一起,它们间无竖直作用力。A与平台水平轨道和小车上表面的动摩擦因数都为0.4,且最大静摩擦力与滑动摩擦力大小相等。物体A、B和小车C的质量均为1kg,取g=10m/s2。求
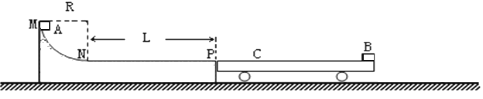
(1)物体A进入N点前瞬间对轨道的压力大小?
(2)物体A在NP上运动的时间?
(3)物体A最终离小车左端的距离为多少?
【答案】(1)物体A进入N点前瞬间对轨道的压力大小为![]() ;
;
(2)物体A在NP上运动的时间为![]()
(3)物体A最终离小车左端的距离为![]()
【解析】试题分析:(1)物体A由M到N过程中,由动能定理得:mAgR=mAvN2
在N点,由牛顿定律得 FN-mAg=mA
联立解得FN=3mAg=30N
由牛顿第三定律得,物体A进入轨道前瞬间对轨道压力大小为:FN′=3mAg=30N
(2)物体A在平台上运动过程中
μmAg=mAa
L=vNt-at2
代入数据解得 t=0.5s t=3.5s(不合题意,舍去)
(3)物体A刚滑上小车时速度 v1= vN-at=6m/s
从物体A滑上小车到相对小车静止过程中,小车、物体A组成系统动量守恒,而物体B保持静止
(mA+ mC)v2= mAv1
小车最终速度 v2=3m/s
此过程中A相对小车的位移为L1,则
![]() 解得:L1=
解得:L1=![]()
物体A与小车匀速运动直到A碰到物体B,A,B相互作用的过程中动量守恒:
(mA+ mB)v3= mAv2
此后A,B组成的系统与小车发生相互作用,动量守恒,且达到共同速度v4
(mA+ mB)v3+mCv2=" (m"A+mB+mC) v4
此过程中A相对小车的位移大小为L2,则
![]() 解得:L2=
解得:L2=![]()
物体A最终离小车左端的距离为x=L1-L2= ![]()