题目内容
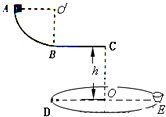 我国成功地发射了“嫦娥一号”探月卫星.卫星进入地球轨道后还需要对卫星进行10次点火控制.前4次点火,让卫星不断变轨加速,当卫星加速到vo=11.0km/s的速度时进入地月转移轨道向月球飞去.后6次点火的主要作用是修正飞行方向和被月球捕获时的紧急刹车,最终把卫星送入离月面h=200km高的工作轨道(可视为匀速圆周运动).已知地球质量是月球质量的81倍,月球和地球的半径分别为:R月=1800km,R地=6400km,卫星质量为2350kg,地球表面重力加速度g=10m/s2,引力恒量G=6.67×10-11N?m2/kg2.求:(结果保留一位有效数字)
我国成功地发射了“嫦娥一号”探月卫星.卫星进入地球轨道后还需要对卫星进行10次点火控制.前4次点火,让卫星不断变轨加速,当卫星加速到vo=11.0km/s的速度时进入地月转移轨道向月球飞去.后6次点火的主要作用是修正飞行方向和被月球捕获时的紧急刹车,最终把卫星送入离月面h=200km高的工作轨道(可视为匀速圆周运动).已知地球质量是月球质量的81倍,月球和地球的半径分别为:R月=1800km,R地=6400km,卫星质量为2350kg,地球表面重力加速度g=10m/s2,引力恒量G=6.67×10-11N?m2/kg2.求:(结果保留一位有效数字)(1)地球的质量.
(2)卫星从离开地球轨道进入地月转移轨道最终稳定在离月球表面h=200km的工作轨道上外力对它做了多少功?(忽略地球自转及月球绕地球公转的影响)
分析:1、忽略地球自转,地球表面的物体受到的重力等于万有引力mg=G
,代入数据可以计算地球的质量.
2、卫星绕月球运动,万有引力提供向心力G
=m
,得v=
,代入数据计算卫星的速度.根据动能定理:W=
mv2-
mv02,代入数据计算即可.
| Mm |
| R地2 |
2、卫星绕月球运动,万有引力提供向心力G
| M月m |
| (R月+h)2 |
| v2 |
| R月+h |
|
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)忽略地球自转,地球表面的物体受到的重力等于万有引力mg=G
,得M=
=
kg=6.14×1024kg
(2)卫星离月球表面h=200km的工作轨道上,万有引力提供向心力G
=m
,
得v=
=
=1590m/s
根据动能定理:W=
mv2-
mv02=
×2350×(15902-110002)J=-1.39×1011J
答:(1)地球的质量为6.14×1024kg.
(2)卫星从离开地球轨道进入地月转移轨道最终稳定在离月球表面h=200km的工作轨道上外力对它做了-1.39×1011J功.
| Mm |
| R地2 |
| gR地2 |
| G |
| 10×(6400×103)2 |
| 6.67×10-11 |
(2)卫星离月球表面h=200km的工作轨道上,万有引力提供向心力G
| M月m |
| (R月+h)2 |
| v2 |
| R月+h |
得v=
|
|
根据动能定理:W=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
答:(1)地球的质量为6.14×1024kg.
(2)卫星从离开地球轨道进入地月转移轨道最终稳定在离月球表面h=200km的工作轨道上外力对它做了-1.39×1011J功.
点评:本题主要考查动能定理和天体运动结合的问题,要主要根据万有引力提供向心力计算出卫星绕月的速度,在运用动能定理计算,难度不大,计算要小心.

练习册系列答案
相关题目
 B.
B.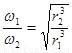
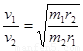 D.
D.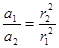
 D.
D.