题目内容
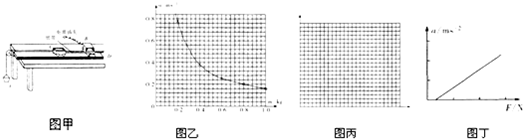
为了探究加速度与力、质量的关系,使用如下图所示的气垫导轨装置进行实验.其中G1、G2为两个光电门,它们与数字计时器相连,当滑行器通过G1、G2光电门时,光束被遮挡的时间△t1、△t2都可以被测量并记录,滑行器连同上面固定的一条形挡光片的总质量为M,挡光片宽度为d,光电门间距为x(满足x>>d),牵引砝码的质量为m.回答下列问题:

(1)若实验测得△t足够小,且△t1=150ms、△t2=100ms,d=3.0cm,X=50.0cm,则滑行器运动的加速度 a=
(2)在(1)中,实际牵引砝码的质量与上述的计算值相比

(1)若实验测得△t足够小,且△t1=150ms、△t2=100ms,d=3.0cm,X=50.0cm,则滑行器运动的加速度 a=
0.05
0.05
m/s2. 若取M=400g,在保证M>>m的条件下,如果认为绳子牵引滑块的力等于牵引砝码的总重力,则牵引砝码的质量m=0.02
0.02
kg.(取g=10m/s2)(2)在(1)中,实际牵引砝码的质量与上述的计算值相比
偏小
偏小
.(填偏大、偏小或相等)分析:(1)由于遮光条通过光电门的时间极短,可以用平均速度表示瞬时速度.根据匀变速直线运动的速度位移公式求出滑块的加速度,M>>m的条件下,合外力等于砝码的重力,则mg=Ma,求出砝码质量;
(2)对M和m整体分析,根据牛顿第二定律求出加速度,从而求出绳子的实际拉力,再与mg比较即可.
(2)对M和m整体分析,根据牛顿第二定律求出加速度,从而求出绳子的实际拉力,再与mg比较即可.
解答:解:(1)由于遮光条通过光电门的时间极短,可以用平均速度表示瞬时速度.
滑块经过光电门1时的瞬时速度v1=
=
=0.2m/s,
滑块经过光电门2时的瞬时速度v2=
=
=0.3m/s.
根据v22-v12=2aX得,
a=
=0.05m/s2;
M>>m的条件下,合外力等于砝码的重力,则mg=Ma,
解得:m=0.002kg;
(2)对M和m整体分析,有:a=
,则绳子的拉力F=Ma=
<mg,所以实际牵引砝码的质量与上述的计算值相比偏小;
故答案为:0.05;0.02;偏小
滑块经过光电门1时的瞬时速度v1=
| d |
| t1 |
| 0.03 |
| 0.15 |
滑块经过光电门2时的瞬时速度v2=
| d |
| t1 |
| 0.03 |
| 0.1 |
根据v22-v12=2aX得,
a=
| (0.3)2-(0.2)2 |
| 2×0.5 |
M>>m的条件下,合外力等于砝码的重力,则mg=Ma,
解得:m=0.002kg;
(2)对M和m整体分析,有:a=
| mg |
| M+m |
| mg | ||
1+
|
故答案为:0.05;0.02;偏小
点评:解决该题关键掌握知道在极短时间内的平均速度可以表示瞬时速度和匀变速直线运动的速度位移公式应用,当m的质量远小于M的质量,m的重力可以认为等于M所受的合力.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 为了探究加速度与力的关系,使用如图所示的气垫导轨装置进行实验.其中G1、G2为两个光电门,它们与数字计时器相连,当滑行器通过G1、G2光电门时,光束被遮挡的时间△t1、△t2都可以被测量并记录,滑行器连同上面固定的一条形挡光片的总质量为M,挡光片宽度为D,光电门间距离为x,牵引砝码的质量为m.
为了探究加速度与力的关系,使用如图所示的气垫导轨装置进行实验.其中G1、G2为两个光电门,它们与数字计时器相连,当滑行器通过G1、G2光电门时,光束被遮挡的时间△t1、△t2都可以被测量并记录,滑行器连同上面固定的一条形挡光片的总质量为M,挡光片宽度为D,光电门间距离为x,牵引砝码的质量为m. 为了探究加速度与力的关系,使用如图所示的气垫导轨装置进行实验.其中G1、G2为两个光电门,它们与数字计时器相连,当滑行器通过G1、G2光电门时,光束被遮挡的时间△t1、△t2都可以被测量并记录,滑行器连同上面固定的一条形挡光片的总质量为M,挡光片宽度为D,光电门间距离为x,牵引砝码的质量为m.回答下列问题:
为了探究加速度与力的关系,使用如图所示的气垫导轨装置进行实验.其中G1、G2为两个光电门,它们与数字计时器相连,当滑行器通过G1、G2光电门时,光束被遮挡的时间△t1、△t2都可以被测量并记录,滑行器连同上面固定的一条形挡光片的总质量为M,挡光片宽度为D,光电门间距离为x,牵引砝码的质量为m.回答下列问题: