��Ŀ����
����Ŀ����ͼ��ʾ����y����Ҳ���ڴŸ�Ӧǿ��ΪB�ķ���ֱֽ���������ǿ�ų�����x����Ϸ���һƽ�а�ʽ���ٵ糡����һ����Ե�������y�ᴦ������ֽ�洹ֱ������һ����Ϊm�������Ϊq�������ɾ�ֹ�������ٵ�ѹΪU�ĵ糡���٣�Ȼ���Դ�ֱ�ڰ�ķ�����ֱ�ߴ�A��������Ե�壬�����x���ϵ�D������x�Ḻ��н�Ϊ30���ķ������������ޣ����ڴ�ʱ��ʩ��һ���糡����ʹ������ֱ�ߵ���y���ϵ�C��(C����ͼ��δ���)����֪OD��Ϊl���������ӵ�����.��

(1)���������Ե��֮ǰ���ٶ�;
(2)���Ӿ�����Ե��ʱ��ʧ�˶��ٶ���;
(3)���ӵ糡�ĵ糡ǿ�Ⱥʹ���������y�ܵ��Ҳ����е���ʱ��.
���𰸡�(1)![]() (2)
(2)![]() (3)
(3)![]()
�������������������1�������ڵ糡�м��٣��ɶ��ܶ����ã� qU��![]() mv2
mv2
��ã�![]() ��
��
��2�������ڴų�����Բ���˶��켣��ͼ��
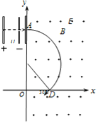
�ɼ��ι�ϵ�ɵù���뾶Ϊ2l��
��![]()
���![]() ��
��
���������غ�ã���ʧ�Ķ�����EK��![]() mv2
mv2![]() mv��2��qU
mv��2��qU![]()
��3����������ֱ���˶�����qv��B=qE
�������ݽ��![]()
������x������б���³�60���ǣ�
�����ڵ�һ����������Բ���˶���ʱ��![]() ��
��
�����ڵ�������������ֱ���˶���ʱ��![]()
����x���Ҳ����е���ʱ��![]()

 ���źþ���Ԫ����ĩ��ϵ�д�
���źþ���Ԫ����ĩ��ϵ�д�