题目内容
将力F分解为F1和F2两个分力,若已知F的大小及F和F2之间的夹角θ,且θ为锐角;则当F1和F2大小相等时,F1的大小为 ;而当F1有最小值时,F2的大小为 .
【答案】分析:因为分力和合力构成矢量三角形,当分力F2与分力F1垂直时,F1最小.
解答:解:将力F分解为F1和F2两个分力,若已知F的大小及F和F2之间的夹角θ,且θ为锐角;
则当F1和F2大小相等时,F1和F2组成菱形,根据几何关系得:
F1的大小为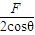 ,
,
因为垂直段最短,知当分力F2与分力F1垂直时,F1最小.如图.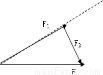 则F2=Fcosθ.
则F2=Fcosθ.
故答案为:18N.
故答案为: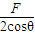 ,Fcosθ
,Fcosθ
点评:解决本题的关键知道合力与分力遵循平行四边形定则(三角形定则),根据作图法可以确定力的最小值.
解答:解:将力F分解为F1和F2两个分力,若已知F的大小及F和F2之间的夹角θ,且θ为锐角;
则当F1和F2大小相等时,F1和F2组成菱形,根据几何关系得:
F1的大小为
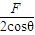 ,
,因为垂直段最短,知当分力F2与分力F1垂直时,F1最小.如图.
 则F2=Fcosθ.
则F2=Fcosθ.故答案为:18N.
故答案为:
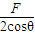 ,Fcosθ
,Fcosθ点评:解决本题的关键知道合力与分力遵循平行四边形定则(三角形定则),根据作图法可以确定力的最小值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目