��Ŀ����
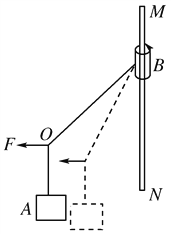
����Ŀ����ͼ��ʾ�����ڴֲ�б���ϵ����A�����ҵ����B�����ھ�ֹ״̬������AO�ƹ��⻬�Ķ����������ʵ��ɵ��Ҷ˼�����BO���϶�������O�㣮���ʵ�����������ˮƽ����������OC������ֱ����ļнǦ�=60�㣬б����Ǧ�=30�㣬���A��B�������ֱ�ΪmA=5kg��mB=1.5kg�����ɵľ���ϵ��Ϊk=500N/m���������ٶ�g=10m/s2 �� ��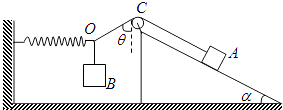
��1�����ɵ��쳤��x��
��2�����A�ܵ���Ħ����f�Ĵ�С�ͷ���
���𰸡�
��1���⣺������OB�����BΪ�о�����������ͼ�������ֽ⣬
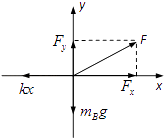
��ƽ��������
x��kx��Fsin60��=0��
y��Fcos60�㩁mBg=0��
�ɢڽ�ã� ![]()
����ٽ�ã� ![]()
�𣺵��ɵ��쳤��xΪ ![]()
��2���⣺���A������ͼ�������ֽ⣬
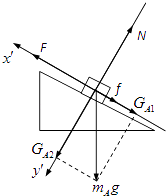
��ƽ��������
x��F��mAgsin30�㩁f=0
��ã� ![]() ��������б������
�������������
�����A�ܵ���Ħ����f�Ĵ�СΪ5N��������б������
����������1��������OB�����BΪ�о�����������ͼ�������ֽ⣬����ƽ��������Ϻ��˶�����⣻��2�������A������ͼ�������ֽ⣬����ƽ��������ʽ��⼴�ɣ�

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ