题目内容
如图所示,两根金属轨道之间的距离为L,轨道水平部分有竖直向上的匀强磁场B,一质量为m的金属杆a在离地h的高处从静止开始沿弧形轨道下滑,一根质量为2 m的金属杆b原来静止放置在水平轨道上,水平轨道足够长,设金属杆a、b不会相碰,金属杆a、b的电阻都是R,其它电阻不计,不计任何摩擦,求:

(1)a和b的最终速度是多大?
(2)当a的速度变为进入磁场时的一半时,a的加速度是多大?
答案:
解析:
解析:
|
解:(1)设金属杆a滑至水平轨道时速率为v1 由机械能守恒,有 得:v1= a进入水平轨道后,发生电磁感应,产生感应电流,使金属杆a、b受到等大反向的安培力,由分析可知,金属杆a、b最终将以相同的速率v2向右运动,把金属杆a、b视为系统,由动量守恒有:mv1=(m+2m)v2(1分) 解得v2= (2)当金属杆a的速度变为原来的一半,即va= a棒产生的感应电动Ea=vaBL(1分),b棒产生的感应电动势Ea=vbBL(1分), 两电动势方向相反,所以回路总电动势E=Ea=-Eb(1分) 流过a棒的电流I= a棒所受安培力为F=IBL(1分) a棒的加速度a= 以上各式联立解得:a= |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
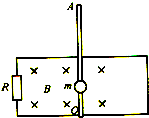 如图所示,两根间距为L的水平金属滑轨处于同一竖直平面内,一端用电阻R相连接,轻金属杆可绕图中的O点贴着滑杆自由转动,摩擦力不计.开始时杆处于竖直位置,杆上固定有一质量为m的小球,杆长2L,小球离O点距离为专,整个装置处于磁感应强度为曰的匀强磁场中,磁场方向如图所示,垂直纸面向里.除R外其余电阻可忽略,滑轨足够长,杆由竖直位置无初速地贴着滑轨向右边倒下,至水平位置时小球的速度为v,试求此过程中通过R的电荷量以及R中的最大电流.
如图所示,两根间距为L的水平金属滑轨处于同一竖直平面内,一端用电阻R相连接,轻金属杆可绕图中的O点贴着滑杆自由转动,摩擦力不计.开始时杆处于竖直位置,杆上固定有一质量为m的小球,杆长2L,小球离O点距离为专,整个装置处于磁感应强度为曰的匀强磁场中,磁场方向如图所示,垂直纸面向里.除R外其余电阻可忽略,滑轨足够长,杆由竖直位置无初速地贴着滑轨向右边倒下,至水平位置时小球的速度为v,试求此过程中通过R的电荷量以及R中的最大电流. ,倾角θ=45°,水平部分处于磁感应强度
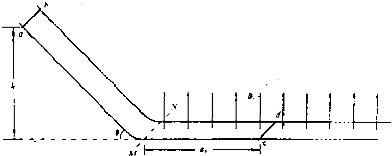
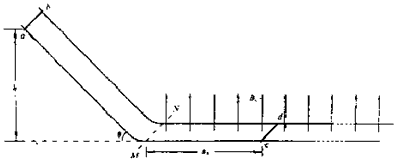
,倾角θ=45°,水平部分处于磁感应强度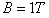 的匀强磁场中,磁场方向竖直向上,磁场左边界MN与导轨垂直。金属棒
的匀强磁场中,磁场方向竖直向上,磁场左边界MN与导轨垂直。金属棒 质量
质量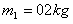 ,电阻
,电阻 ,金属棒
,金属棒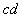 质量
质量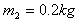 ,电阻
,电阻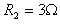 ,导轨电阻不计,两棒与导轨间动摩擦因数
,导轨电阻不计,两棒与导轨间动摩擦因数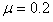 。开始时,棒
。开始时,棒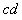 放在斜导轨上,与水平导轨高度差
放在斜导轨上,与水平导轨高度差 ,棒
,棒 。两棒均与导轨垂直,现将棒
。两棒均与导轨垂直,现将棒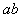 由静止释放,取
由静止释放,取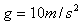 。求:
。求:  运动到MN处的速度大小;
运动到MN处的速度大小; 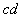 运动的最大加速度;
运动的最大加速度; 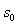 。
。 
 的匀强磁场中,磁场方向竖直向上,磁场左边界MN与导轨垂直。金属棒
的匀强磁场中,磁场方向竖直向上,磁场左边界MN与导轨垂直。金属棒
