题目内容
4.春分时,阳光直射赤道,现赤道上有一个人在日落后2小时,抬头发现在头顶正上方有一颗卫星,设地球半径为R,则该卫星离地面高度至少为$(\frac{2}{\sqrt{3}}-1)R$,若该卫星绕地球转动方向与地球自转方向相同,它离地比同步卫星离地更远,则从地面上看它的运动方向为自东向西(填“自东向西”或“自西向东”).分析 赤道上有一个人在日落后2小时,抬头发现在头顶正上方有一颗卫星,2h地球转动30°,画出光路图,结合几何关系分析卫星的最小高度;如果卫星的高度大于同步卫星,利用万有引力等于向心力列式求解出角速度的表达式分析即可.
解答 解:春分时,阳光直射赤道,现赤道上有一个人在日落后2小时,抬头发现在头顶正上方有一颗卫星,光路图如图所示: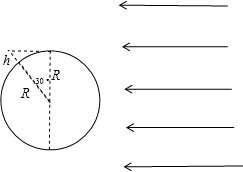
结合几何关系,有:
h=$\frac{R}{cos30°}-R$=$(\frac{2}{\sqrt{3}}-1)R$
对于卫星,万有引力提供向心力,故:
$G\frac{Mm}{{r}^{2}}=m{ω}^{2}r$
解得:
ω=$\sqrt{\frac{GM}{{r}^{3}}}$
故如果卫星的高度大于同步卫星,则轨道半径大于同步卫星,则角速度小于同步卫星,故从地面上看它的运动方向为自东向西;
故答案为:$(\frac{2}{\sqrt{3}}-1)R$,自东向西.
点评 本题第一问关键是结合地球的转动情况,画出光路图分析,注意太阳光当作平行光分析;第二问考虑卫星间的相对转动情况即可.

练习册系列答案
相关题目
15.利用回旋加速器加速带电粒子时,下列说法正确的是( )
| A. | 电场用来加速带电粒子,磁场则使带电粒子回旋 | |
| B. | 电场和磁场同时用来加速带电粒子 | |
| C. | 加速电压越大,同一带电粒子最终获得的动能就越大 | |
| D. | 在回旋加速器的半径一定的情况下,所加磁场越强,同一带电粒子最终获得的动能就越大 |
12. 1932年,劳伦斯和利文斯顿设计出了回旋加速器.回旋加速器的工作原理如图所示,置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过的时间可以忽略不计.磁感应强度为B的匀强磁场与盒面垂直.A处粒子源产生初速度不计、质量为m、电荷量为+q的粒子.粒子在加速器中被加速,加速电压为U.加速过程中不考虑相对论效应和重力作用.关于回旋加速器,下列说法正确的是( )
1932年,劳伦斯和利文斯顿设计出了回旋加速器.回旋加速器的工作原理如图所示,置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过的时间可以忽略不计.磁感应强度为B的匀强磁场与盒面垂直.A处粒子源产生初速度不计、质量为m、电荷量为+q的粒子.粒子在加速器中被加速,加速电压为U.加速过程中不考虑相对论效应和重力作用.关于回旋加速器,下列说法正确的是( )
 1932年,劳伦斯和利文斯顿设计出了回旋加速器.回旋加速器的工作原理如图所示,置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过的时间可以忽略不计.磁感应强度为B的匀强磁场与盒面垂直.A处粒子源产生初速度不计、质量为m、电荷量为+q的粒子.粒子在加速器中被加速,加速电压为U.加速过程中不考虑相对论效应和重力作用.关于回旋加速器,下列说法正确的是( )
1932年,劳伦斯和利文斯顿设计出了回旋加速器.回旋加速器的工作原理如图所示,置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过的时间可以忽略不计.磁感应强度为B的匀强磁场与盒面垂直.A处粒子源产生初速度不计、质量为m、电荷量为+q的粒子.粒子在加速器中被加速,加速电压为U.加速过程中不考虑相对论效应和重力作用.关于回旋加速器,下列说法正确的是( )| A. | 带电粒子从磁场中获得能量 | |
| B. | D形盒的半径R越大,粒子加速所能获得的最大动能越大 | |
| C. | 交变电源的加速电压U越大,粒子加速所能获得的最大动能越大 | |
| D. | 粒子第2次和第1次经过两D形盒间狭缝后轨道半径之比为$\sqrt{2}$:1 |
19. 如图为哈勃望远镜拍摄的银河系中被科学家称为“罗盘座T星”系统的照片,该系统是由一颗白矮星和它的类日伴星组成的双星系统,图片下面的亮点为白矮星,上面的部分为类日伴星(中央的最亮的为类似太阳的天体).由于白矮星不停地吸收由类日伴星抛出的物质致使其质量不断增加,科学家预计这颗白矮星在不到1000万年的时间内会完全“爆炸”,从而变成一颗超新星.现假设类日伴星所释放的物质被白矮星全部吸收,并且两星之间的距离在一段时间内不变,两星球的总质量不变,不考虑其它星球对该“罗盘座T星”系统的作用,则下列说法正确的是( )
如图为哈勃望远镜拍摄的银河系中被科学家称为“罗盘座T星”系统的照片,该系统是由一颗白矮星和它的类日伴星组成的双星系统,图片下面的亮点为白矮星,上面的部分为类日伴星(中央的最亮的为类似太阳的天体).由于白矮星不停地吸收由类日伴星抛出的物质致使其质量不断增加,科学家预计这颗白矮星在不到1000万年的时间内会完全“爆炸”,从而变成一颗超新星.现假设类日伴星所释放的物质被白矮星全部吸收,并且两星之间的距离在一段时间内不变,两星球的总质量不变,不考虑其它星球对该“罗盘座T星”系统的作用,则下列说法正确的是( )
 如图为哈勃望远镜拍摄的银河系中被科学家称为“罗盘座T星”系统的照片,该系统是由一颗白矮星和它的类日伴星组成的双星系统,图片下面的亮点为白矮星,上面的部分为类日伴星(中央的最亮的为类似太阳的天体).由于白矮星不停地吸收由类日伴星抛出的物质致使其质量不断增加,科学家预计这颗白矮星在不到1000万年的时间内会完全“爆炸”,从而变成一颗超新星.现假设类日伴星所释放的物质被白矮星全部吸收,并且两星之间的距离在一段时间内不变,两星球的总质量不变,不考虑其它星球对该“罗盘座T星”系统的作用,则下列说法正确的是( )
如图为哈勃望远镜拍摄的银河系中被科学家称为“罗盘座T星”系统的照片,该系统是由一颗白矮星和它的类日伴星组成的双星系统,图片下面的亮点为白矮星,上面的部分为类日伴星(中央的最亮的为类似太阳的天体).由于白矮星不停地吸收由类日伴星抛出的物质致使其质量不断增加,科学家预计这颗白矮星在不到1000万年的时间内会完全“爆炸”,从而变成一颗超新星.现假设类日伴星所释放的物质被白矮星全部吸收,并且两星之间的距离在一段时间内不变,两星球的总质量不变,不考虑其它星球对该“罗盘座T星”系统的作用,则下列说法正确的是( )| A. | 两星之间的万有引力不变 | B. | 两星的运动周期不变 | ||
| C. | 类日伴星的轨道半径减小 | D. | 白矮星的线速度变小 |
16.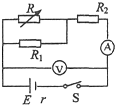 如图所示的电路中,电源电动势为E,内阻为r(R2<r<R1+R2),电表均视为理想电表.闭合开关S后,调节R的阻值,使电流表的示数增大△I,在这一过程中电压表示数的变化量的大小为△U,则( )
如图所示的电路中,电源电动势为E,内阻为r(R2<r<R1+R2),电表均视为理想电表.闭合开关S后,调节R的阻值,使电流表的示数增大△I,在这一过程中电压表示数的变化量的大小为△U,则( )
 如图所示的电路中,电源电动势为E,内阻为r(R2<r<R1+R2),电表均视为理想电表.闭合开关S后,调节R的阻值,使电流表的示数增大△I,在这一过程中电压表示数的变化量的大小为△U,则( )
如图所示的电路中,电源电动势为E,内阻为r(R2<r<R1+R2),电表均视为理想电表.闭合开关S后,调节R的阻值,使电流表的示数增大△I,在这一过程中电压表示数的变化量的大小为△U,则( )| A. | 通过R的电流增大,但增大量小于△I | B. | $\frac{△U}{△I}$的大小随R的变化而变化 | ||
| C. | 电源的输出功率一定增大了 | D. | 电源的效率降低了$\frac{△I•r}{E}$ |
13. 如图所示的电路中,电源电动势为E、内阻为r=0,R2=3R1,R3=R4.当R2的滑动片P从最右端向最左端滑动的过程中,下列说法正确( )
如图所示的电路中,电源电动势为E、内阻为r=0,R2=3R1,R3=R4.当R2的滑动片P从最右端向最左端滑动的过程中,下列说法正确( )
 如图所示的电路中,电源电动势为E、内阻为r=0,R2=3R1,R3=R4.当R2的滑动片P从最右端向最左端滑动的过程中,下列说法正确( )
如图所示的电路中,电源电动势为E、内阻为r=0,R2=3R1,R3=R4.当R2的滑动片P从最右端向最左端滑动的过程中,下列说法正确( )| A. | 电容器先放电,后充电 | |
| B. | 导线EF上的电流方向始终从F到E | |
| C. | 电容器的最大电荷量为$\frac{EC}{2}$ | |
| D. | 电容器上板的电势总比下板的电势低 |
14.如图所示是一支旅行用的“两面针”牙膏,该牙膏的外壳是由铝薄皮做的,根据你的观察和生活经验,下列说法正确的是( )


| A. | 牙膏盖上的条纹是为了增大摩擦 | |
| B. | 牙膏被挤出来是因为牙膏受到手的作用力 | |
| C. | 该牙膏皮被挤压后发生的形变为非弹性形变 | |
| D. | 挤牙膏时手对牙膏皮的作用力与牙膏皮对手的作用力二力平衡 |
 为了把陷在泥坑里的汽车拉出来,司机用一条结实的绳子把汽车拴在一棵大树上,开始时相距12m,然后在绳的中点用200N的力F,沿与绳垂直的方向拉绳,结果中点被拉过60cm.如图所示,假设绳子的伸长可以不计,求这时汽车受到的拉力.
为了把陷在泥坑里的汽车拉出来,司机用一条结实的绳子把汽车拴在一棵大树上,开始时相距12m,然后在绳的中点用200N的力F,沿与绳垂直的方向拉绳,结果中点被拉过60cm.如图所示,假设绳子的伸长可以不计,求这时汽车受到的拉力.