��Ŀ����
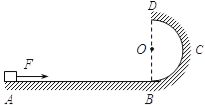
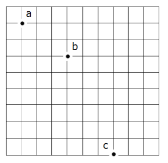
����Ŀ����ͼ����ʾ���ڱ߽�MN���ռ������ͼ����ʾ�����Ա仯����ǿ�ų����涨�ų���ֱֽ������Ϊ������һ������Ϊm�������Ϊ+q��������ˮƽ���ٶ�v0��x������������ֱ���˶���t��0ʱ�̣����Ӹվ�������ԭ��O��֮�����ڴų�����ʹ�������ٴ�ͨ��O��ʱ�ٶȷ�����x�Ḻ�����60���������·�����֪�ų��߽�MN��ֱ�߷���Ϊx=4L�������������������Դų��仯������Ӱ�졣��B0��Сδ֪����


��1��t1��t0Ӧ����ʲô��ϵ��
��2��������ͨ��O�������������˶�����t0С�������ڴų�����Բ���˶������ڡ��������ڴų����˶������ڲ��ᳬ�����
��3�����㣨2��������B0ӦΪ���٣�
���𰸡�(1) ![]() (n=0, 1, 2, 3 ������ ) (2) T=
(n=0, 1, 2, 3 ������ ) (2) T=![]() (3) B0��
(3) B0��![]()
��������
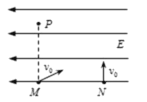
(1)�����˶��켣��ͼ��ʾ��
������t1ʱ����Ӧ������ֱ���˶���t0ʱ����������Բ���˶���ƫת2n��+4��/3
��������v0t1=OP=![]() v0t0=n2��r+4��r/3
v0t0=n2��r+4��r/3
�����ɵã�![]() (n=0, 1, 2, 3 ������ )
(n=0, 1, 2, 3 ������ )
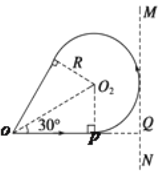
(2) �������˶��иպú�ֱ��MN����ʱ�������˶������ڴﵽ���ʱ����Բ���˶��İ뾶���
�����뾶ΪR����ͼ�м��ι�ϵ֪ R+![]() R=4L
R=4L
��R= ![]()
����Բ���˶����ٹ�O�㣬���˶��켣��ͼ��
����v0t1 ��![]() R v0t0 = 4��R/3
R v0t0 = 4��R/3
�����˶����������T��ͼ��֪Ϊ��T=6t1+3t0
��ã�T= ![]()
(3) ��С���˶����������ʱ����ţ�ٵڶ������У�![]()
��ã�B0��![]()

 ��Ȥ������ҵ���ϿƼ�������ϵ�д�
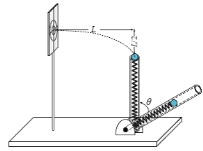
��Ȥ������ҵ���ϿƼ�������ϵ�д�����Ŀ��һ��ͬѧ����ͼ1��ʾ��װ���о�������һ��ʱ�����ٶ������Ĺ�ϵ����
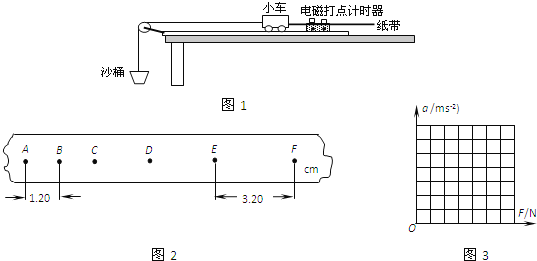
(1)ʵ���У��������С�������������룩����______ ɳͰ����ɳ������������ΪС���ܵ�����F����ɳͰ������ɳ����������ͨ������ֽ���õ�С���˶��ļ��ٶ�a�Ĵ�С����ȷʹ�õ�Ŵ���ʱ���������ijһ��ֽ����ͼ��A��B��C��D��E��F��6�������㣬���ڼ�����仹���ĸ���δ���������ͼ2�и��������ݿ����С���ļ��ٶ�a=______m/s2��B����ٶ�vB=______m/s��
(2)����ͬѧ����ͼ3��ʾװ�ã���ö���С����������F�ͼ��ٶ�a�����ݣ����±���
F/N | 0.21 | 0.30 | 0.40 | 0.49 | 0.60 |
a/��ms-2�� | 0.10 | 0.21 | 0.29 | 0.41 | 0.49 |
�����ݲ�õ����ݣ���ͼ������a-Fͼ��
��___________��
����ͼ���֪��С���볤ľ��֮������Ħ������СΪ______N��