题目内容
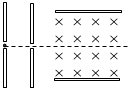 如图所示,从s处发出的热电子(初速为零)经加速电压U加速后垂直进入相互垂直的匀强电场和匀强磁场中,发现电子向上极板偏转.设两极板间电场强度为E,磁感强度为B.为使电子沿直线从该混合场区域通过,可采取以下哪些措施( )
如图所示,从s处发出的热电子(初速为零)经加速电压U加速后垂直进入相互垂直的匀强电场和匀强磁场中,发现电子向上极板偏转.设两极板间电场强度为E,磁感强度为B.为使电子沿直线从该混合场区域通过,可采取以下哪些措施( )分析:根据eU=
mv2可得v=
;粒子在复合场中若做匀速直线运动的条件是:Eq=qvB.
根据左手定则可知电子所受的洛伦兹力的方向竖直向下,故电子向上极板偏转的原因是电场力大于洛伦兹力,因此要么电场力变小,要么洛伦兹力变大.
| 1 |
| 2 |
|
根据左手定则可知电子所受的洛伦兹力的方向竖直向下,故电子向上极板偏转的原因是电场力大于洛伦兹力,因此要么电场力变小,要么洛伦兹力变大.
解答:解:要使粒子在复合场中做匀速直线运动,故Eq=qvB.
根据左手定则可知电子所受的洛伦兹力的方向竖直向下,故电子向上极板偏转的原因是电场力大于洛伦兹力,所以要么增加洛伦兹力,要么减小电场力.
A、适当减小电场强度E,即可以减小电场力,故A正确.
B、适当减小磁感强度B,可以减小洛伦兹力,故B错误.
C、适当增大加速电场极板之间的距离,根据eU=
mv2可得v=
;由于粒子两者间的电压没有变化,所以电子进入磁场的速率没有变化,因此没有改变电场力和洛伦兹力的大小,故C错误.
D、根据eU=
mv2可得v=
;故适当粒子增加加速电压U,可以增加电子在复合场中运动的速度v,从而增加洛伦兹力.故D正确.
故选AD.
根据左手定则可知电子所受的洛伦兹力的方向竖直向下,故电子向上极板偏转的原因是电场力大于洛伦兹力,所以要么增加洛伦兹力,要么减小电场力.
A、适当减小电场强度E,即可以减小电场力,故A正确.
B、适当减小磁感强度B,可以减小洛伦兹力,故B错误.
C、适当增大加速电场极板之间的距离,根据eU=
| 1 |
| 2 |
|
D、根据eU=
| 1 |
| 2 |
|
故选AD.
点评:本题是综合性较强的题目,物体的运动分成两个阶段:在电场中的加速和在复合场中的匀速直线运动.在解题时要注意过程分析和受力分析.

练习册系列答案
相关题目
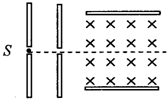 如图所示,从S处发出的热电子(初速度为零),经加速电压U加速后垂直进入相互垂直的匀强电场和匀强磁场中,已知电场强度为E,方向竖直向下,磁感应强度为B,方向垂直纸面向里,现发现电子向上极板偏转,为使电子沿图中虚线从该混合场区域通过,可采取的措施有( )
如图所示,从S处发出的热电子(初速度为零),经加速电压U加速后垂直进入相互垂直的匀强电场和匀强磁场中,已知电场强度为E,方向竖直向下,磁感应强度为B,方向垂直纸面向里,现发现电子向上极板偏转,为使电子沿图中虚线从该混合场区域通过,可采取的措施有( )| A、适当减少电场强度E | B、适当增大磁感应强度B | C、适当增大加速极板间的宽度 | D、适当增大加速电压U |
 如图所示,从S处发出的热电子经加速电压U加速后垂直进入相互垂直的匀强电场和匀强磁场中,发现电子流向上极板偏转.设两极板间电场强度为E,磁感应强度为B.欲使电子沿直线从电场和磁场区域通过,只采取下列措施,其中可行的是( )
如图所示,从S处发出的热电子经加速电压U加速后垂直进入相互垂直的匀强电场和匀强磁场中,发现电子流向上极板偏转.设两极板间电场强度为E,磁感应强度为B.欲使电子沿直线从电场和磁场区域通过,只采取下列措施,其中可行的是( ) 如图所示,从S 处发出的热电子(初速为零)经加速电压U加速后垂直进入相互垂直的匀强电场和匀强磁场中,发现电子向上极板偏转.设两极板间电场强度为E,磁感强度为B.为使电子沿直线从该混合场区域通过,可采取以下哪个措施( )
如图所示,从S 处发出的热电子(初速为零)经加速电压U加速后垂直进入相互垂直的匀强电场和匀强磁场中,发现电子向上极板偏转.设两极板间电场强度为E,磁感强度为B.为使电子沿直线从该混合场区域通过,可采取以下哪个措施( ) 如图所示,从S处发出的热电子经加速电压U加速后垂直进入相互垂直的匀强电场和匀强磁场中,发现电子流向下极板偏转.设两极板间电场强度为E,磁感应强度为B.如果要使电子沿直线从电场和磁场区域通过,以下办法可行的是( )
如图所示,从S处发出的热电子经加速电压U加速后垂直进入相互垂直的匀强电场和匀强磁场中,发现电子流向下极板偏转.设两极板间电场强度为E,磁感应强度为B.如果要使电子沿直线从电场和磁场区域通过,以下办法可行的是( )