题目内容
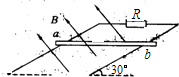
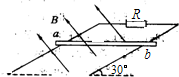如图所示，在一对平行的金属导轨的上端连接一阻值为R的定值电阻，两导轨所决定的平面与水平面成30°角，若将一质量为m、长为L的导体棒ab垂直于两导轨放在导轨上，并使其由静止开始下滑，已知导体棒电阻为r，整个装置处在垂直于导轨平面的匀强磁场中，磁感应强度为B，求导体棒最终下滑的速度及电阻R最终的发热功率分别为多少．（导轨足够长，磁场足够大，不计导轨电阻和摩擦）分析：（1）金属棒下滑时切割磁感线运动，产生感应电动势，产生感应电流，受到沿斜面向上的安培力，做加速度逐渐减小的加速运动，当加速度为0时，速度最大．
（2）下滑过程中，重力势能减小，动能增加，内能增加，根据能量守恒求出整个电路产生的热量，从而求出电阻R上产生的热量．
（2）下滑过程中，重力势能减小，动能增加，内能增加，根据能量守恒求出整个电路产生的热量，从而求出电阻R上产生的热量．
解答：
解：导体棒由静止释放后，加速下滑，受力情况如图所示，由右手定则判定棒中电流方向由b→a，由左手定则判定，受安培力沿斜面向上，随着棒的下滑速度不断增大，安培力F增大，加速度减小，导体棒做变加速运动，当加速度a=0时，速度达到最大，即最终下滑速度，此时导体棒受力平衡，有
mgsin30°=F=BIL①
其中I=
=
②
由①②解得vm=
热功率P=I2R=(
)2R=
答：导体棒最终下滑的速度为vm=
及电阻R最终的发热功率为
．
解：导体棒由静止释放后，加速下滑，受力情况如图所示，由右手定则判定棒中电流方向由b→a，由左手定则判定，受安培力沿斜面向上，随着棒的下滑速度不断增大，安培力F增大，加速度减小，导体棒做变加速运动，当加速度a=0时，速度达到最大，即最终下滑速度，此时导体棒受力平衡，有mgsin30°=F=BIL①
其中I=
| E |
| R+r |
| BLvm |
| R+r |
由①②解得vm=
| mg(R+r) |
| 2B2L2 |
热功率P=I2R=(
| mg |
| 2BL |
| m2g2R |
| 4B2L2 |
答：导体棒最终下滑的速度为vm=
| mg(R+r) |
| 2B2L2 |
及电阻R最终的发热功率为
| m2g2R |
| 4B2L2 |
点评：本题还可以这样解：
当棒匀速下滑时，重力做正功，安培力做负功，导体棒的重力势能的减少等于回路中电能的增加，
PG=P电，即mgvmsin30°=
①
其中E=BLvm②
由①②得vm=
由R和r串联，功率分配关系为PR=
P电=
mgvmsin30°=
注意电路中产生的电功率不全是电阻R消耗的电功率．
当棒匀速下滑时，重力做正功，安培力做负功，导体棒的重力势能的减少等于回路中电能的增加，
PG=P电，即mgvmsin30°=
| E2 |
| R+r |
其中E=BLvm②
由①②得vm=
| mg(R+r) |
| 2B2L2 |
由R和r串联，功率分配关系为PR=
| R |
| R+r |
| R |
| R+r |
| m2g2R |
| 4B2L2 |
注意电路中产生的电功率不全是电阻R消耗的电功率．
练习册系列答案
相关题目
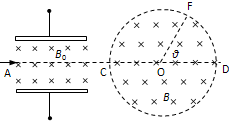如图所示，有一对平行金属板，两板相距为0.05m．电压为10V；两板之间有匀强磁场，磁感应强度大小为B0=0.1T，方向与金属板面平行并垂直于纸面向里．图中右边有一半径R为0.1m、圆心为O的圆形区域内也存在匀强磁场，磁感应强度大小为
