题目内容
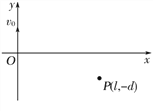
【题目】如图在坐标系xOy里，有质量为m，电荷量为＋q的粒子从原点O沿y轴正方向以初速度v0射出，现要求该粒子能通过点P(l，－d)，可通过在粒子运动的空间范围内加适当的“场”来实现，粒子重力忽略不计(静电力常量为k)。
(1)若只在x轴上某点固定一带负电的点电荷Q，使粒子在点电荷产生的电场中做匀速圆周运动，并能到达P点，求点电荷Q的电荷量大小；
(2)若在整个Ⅰ、Ⅱ象限内加垂直纸面向外的匀强磁场，并在第Ⅳ象限内加平行于x轴，沿x轴正方向的匀强电场，也能使粒子运动到达P点。如果此过程中粒子在电、磁场中运动的时间相等，求磁感应强度B的大小和电场强度E的大小。
【答案】（1）
（2）
【解析】(1) 粒子由O到P的轨迹如图所示，粒子在电场中做圆周运动，半径为R1，由几何关系知：
(l－R1)2＋d2＝R12， 得： 
①
由牛顿第二定律可知： 
得： 
②
(2)粒子由O经P′到P的轨迹如图所示，粒子在磁场中做圆周运动，在电场中做类平抛运动。
在电场中运动时间
，在磁场中运动时间
，
由此得： 
③
在磁场中做圆周运动，设半径为R2，
则有v0t＝πR2， 得： 
，
电场中P′P″＝l－2R2＝l－
， 
，
由此得： 
④
名校课堂系列答案
【题目】某同学利用竖直上抛小球的频闪照片验证机械能守恒定律。频闪仪每隔0.05s 闪光一次，用毫米刻度尺测得相邻两个时刻小球上升的高度分别为s1=26.3cm，s2=23.68cm，s3=21.16cm，s4=18.66cm，s5=16.04cm，该同学通过计算得到不同时刻的速度如下表所示（当地重力加速度g=9.80m/s2，小球质量m=0.10kg）：
时刻 |
|
|
|
|
速度（m/s） | 4.48 | 3.98 | 3.47 |
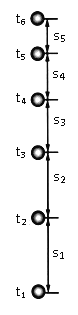
（1）上面测量高度的五个数据中不符合有效数字读数要求的是 段，应记作 cm；
（2）由频闪照片上的数据计算t2时刻小球的速度
＝__________m/s；(计算结果保留三位有效数字）
（3）从t2到t5时间内，重力势能增量
＝_________J，动能减少量
＝________J；（计算结果保留三位有效数字）
（4）在误差允许的范围内，若
与
近似相等，从而验证了机械能守恒定律。由上述计算所得_____（选填“>”、“<”或“＝”），造成这种结果的主要原因是 。