题目内容
 (2005?徐州二模)如图所示,ab面水平,bc是位于竖直平面内的半圆形光滑轨道,半径R=0.225m 在b点与水平面相切,滑块从水平轨道上距离b点1.2m的a点以初速发v0=6m/s运动,经过水平和半圆轨道后从最高点c飞出,最后刚好落回轨道上的a点 取重力加速度g:10m/s2.求:
(2005?徐州二模)如图所示,ab面水平,bc是位于竖直平面内的半圆形光滑轨道,半径R=0.225m 在b点与水平面相切,滑块从水平轨道上距离b点1.2m的a点以初速发v0=6m/s运动,经过水平和半圆轨道后从最高点c飞出,最后刚好落回轨道上的a点 取重力加速度g:10m/s2.求:(1)滑块从c点飞出时速度的大小;
(2)水平轨道与滑块间的动摩擦因数.
分析:(1)滑块从c点飞出后作平抛运动,根据平抛运动的基本公式即可求解速度;
(2)对于滑块从b到c的运动过程,由机械能守恒定律求得b点速度,对于滑块从a到b的运动过程,由动能定理即可求解μ.
(2)对于滑块从b到c的运动过程,由机械能守恒定律求得b点速度,对于滑块从a到b的运动过程,由动能定理即可求解μ.
解答:解:(1)滑块从c点飞出后作平抛运动,其飞行时间为t,则
t=
=0.3s
所以vc=
=
=4m/s
(2)对于滑块从b到c的运动过程,由机械能守恒定律得:
mvc2+mgh=
mvb2
解得 vb=5m/s
对于滑块从a到b的运动过程,设动摩擦因数为μ,由动能定理得:
-μmgs=
mvb2-
mv02
解得μ=0.46
答:(1)滑块从c点飞出时速度的大小为4m/s;
(2)水平轨道与滑块间的动摩擦因数为0.46.
t=
|
所以vc=
| x |
| t |
| 1.2 |
| 0.3 |
(2)对于滑块从b到c的运动过程,由机械能守恒定律得:
| 1 |
| 2 |
| 1 |
| 2 |
解得 vb=5m/s
对于滑块从a到b的运动过程,设动摩擦因数为μ,由动能定理得:
-μmgs=
| 1 |
| 2 |
| 1 |
| 2 |
解得μ=0.46
答:(1)滑块从c点飞出时速度的大小为4m/s;
(2)水平轨道与滑块间的动摩擦因数为0.46.
点评:本题主要考查了平抛运动基本公式、动能定理、机械能守恒定律的直接应用,要求同学们清楚物体运动过程,难度适中.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
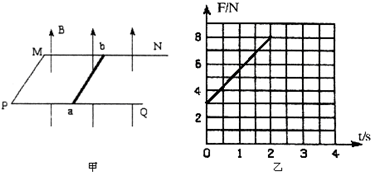
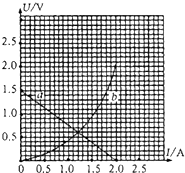 (2005?徐州二模)某同学在实验室先后完成下面二个实验:①测定一节干电池的电动势和内电阻;②描绘小灯泡的伏安特性曲线.
(2005?徐州二模)某同学在实验室先后完成下面二个实验:①测定一节干电池的电动势和内电阻;②描绘小灯泡的伏安特性曲线.
 (2005?徐州二模)如图所示,在粗糙绝缘水平面上固定两个等量同种电荷P、Q,在PQ连线上的M点由静止释放一带电滑块,则滑块会由静止开始一直向右运动到PQ连线上的另一点N而停下,则滑块由M到N的过程中,以下说法正确的是( )
(2005?徐州二模)如图所示,在粗糙绝缘水平面上固定两个等量同种电荷P、Q,在PQ连线上的M点由静止释放一带电滑块,则滑块会由静止开始一直向右运动到PQ连线上的另一点N而停下,则滑块由M到N的过程中,以下说法正确的是( )