题目内容
如图所示,一个矩形线圈的ab、cd边长为L1,ad、bc边长为L2,线圈的匝数为N,线圈处于磁感应强度为B的匀强磁场中, 并以OO/为中轴做匀速圆周运动,(OO/与磁场方向垂直,线圈电阻不计),线圈转动的角速度为ω,设转动从中性面开始计时,请回答下列问题:
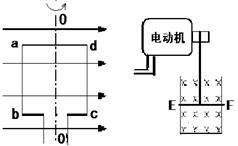
(1)请用法拉第电磁感应定律证明该线圈产生的是正弦交流电。
(2)将线圈产生的交流电通入电阻为R的电动机时,形成的电流有效值为I,请计算该电动机的输出的机械功率(其它损耗不计)。
(3)用此电动机将竖直固定的光滑U型金属框架上的水平导体棒EF从静止向上拉,已知导体棒的质量为m,U型金属框架宽为L且足够长,内有垂直向里的匀强磁场,磁感应强度为B0,导体棒上升高度为h时,经历的时间为t,且此时导体棒刚开始匀速上升,棒有效电阻为R0,金属框架的总电阻不计,棒与金属框架接触良好,请计算:
①导体棒匀速上升时的速度和已知量的关系。
②若t时刻导体棒的速度为v0,求t时间内导体棒与金属框架产生的焦耳热。
(1)证明见解析。
(2)P=![]() -I2R
-I2R
(3)①![]() -I2R= mgv+
-I2R= mgv+![]()
②Q=(![]() -I2R)t-mgh-
-I2R)t-mgh-![]() mv02
mv02
解析:
(1)(6分)证明:如图所示,边长L1切割磁感线产生电动势

e1=BL1V⊥=BL1Vsinωt 而线速度V=![]()
∴ e1=BL1![]() sinωt 因有两个边切割,且有N匝
sinωt 因有两个边切割,且有N匝
∴ e=2N e1=NBL1L2ωsinωt 即:e=Emsinωt
(2)次电流通过电动机时,输入的功率
![]()
由能量守恒知: P入=PQ+P(P为机械功率)
∴P=![]() -I2R (5分)
-I2R (5分)
(3)①(5分)电机带导体棒匀
速上升。受力如图
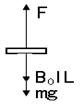
F=B0IL+mg I= ![]() ,F=
,F=![]()
∴![]() =mg+
=mg+![]()
即:![]() -I2R= mgv+
-I2R= mgv+![]()
②(5分)对上升h应用动能定理:Pt-W-mgh=![]() mv02-0
mv02-0
Q=W= Pt-mgh-![]() mv02
mv02
Q=(![]() -I2R)t-mgh-
-I2R)t-mgh-![]() mv02
mv02

如图所示,一个矩形线框从匀强磁场的上方自由落下,进入匀强磁场中,然后再从磁场中穿出。已知匀强磁场区域的宽度大于线框的高度h,那么下列说法中正确的是:( )
| A.线框只在进入和穿出磁场的过程中,才有感应电流产生 |
| B.线框从进入到穿出磁场的整个过程中,都有感应电流产生 |
| C.线框在进入和穿出磁场的过程中,都是机械能变成电能 |
| D.整个线框都在磁场中运动时,机械能转变成内能 |
 如图所示,一个矩形线框,面积为S,线框平面与磁感应强度为B的匀强磁场方向垂直,则此时穿过线框的磁通量Φ=
如图所示,一个矩形线框,面积为S,线框平面与磁感应强度为B的匀强磁场方向垂直,则此时穿过线框的磁通量Φ= (2007?滨州一模)如图所示,一个矩形线框从匀强磁场的上方自由落下,进入匀强磁场中,然后再从磁场中穿出,已知匀强磁场区域的宽度L大于线框的高度h,则下列说法正确的是( )
(2007?滨州一模)如图所示,一个矩形线框从匀强磁场的上方自由落下,进入匀强磁场中,然后再从磁场中穿出,已知匀强磁场区域的宽度L大于线框的高度h,则下列说法正确的是( )
