题目内容
15.有一根细长而均匀的金属管线样品,长约为60cm,电阻大约为6Ω.横截面如图甲所示.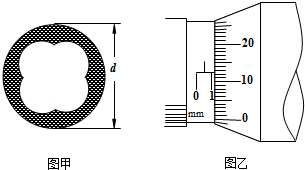
(1)用螺旋测微器测量金属管线的外径,示数如图乙所示,金属管线的外径为1.125mm;
(2)现有如下器材
A.电流表(量程0.6A,内阻约0.1Ω)
B.电流表(量程3A,内阻约0.03Ω)
C.电压表(量程3V,内阻约3kΩ)
D.滑动变阻器(1750Ω,0.3A)
E.滑动变阻器(15Ω,3A)
F.蓄电池(6V,内阻很小)
G.开关一个,带夹子的导线若干
要进一步精确测量金属管线样品的阻值,电流表应选A,滑动变阻器应选E.(只填代号字母).
(3)已知金属管线样品材料的电阻率为ρ,通过多次测量得出金属管线的电阻为R,金属管线的外径为d,要想求得金属管线内形状不规则的中空部分的截面积S,在前面实验的基础上,还需要测量的物理量是管线长度L(所测物理量用字母表示并用文字说明).计算中空部分截面积的表达式为S=$\frac{{π{d^2}}}{4}-\frac{ρL}{R}$.
分析 (1)螺旋测微器的读数等于固定刻度读数加上可动刻度读数,在读可动刻度读数时需估读.
(2)根据电路中电流的大小确定电流表的量程,从测量误差的角度选择滑动变阻器.
(3)根据电阻定律求出导体电阻的横截面积,用大圆的面积减去电阻的横截面积,即为中空部分的截面积.
解答 解:(1)螺旋测微器的读数等于1mm+0.01×12.5mm=1.125mm.
(2)电路中的电流大约为:I=$\frac{3}{6}A=0.5A$,所以电流表选择A.待测电阻较小,若选用大电阻滑动变阻器,测量误差角度,所以滑动变阻器选择E.
(3)还需要测量的物理量是管线长度L,根据R=$ρ\frac{L}{S}$,则S=$\frac{ρL}{R}$,则中空部分的截面积为:$S′=\frac{π{d}^{2}}{4}-S=\frac{π{d}^{2}}{4}-\frac{ρL}{R}$.
故答案为:①1.125;(2)A,E;(3)管线长度L,$\frac{{π{d^2}}}{4}-\frac{ρL}{R}$
点评 解决本题的关键掌握螺旋测微器的读数方法,以及掌握电阻定律的公式,掌握如何确定电流表的内外接.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.一皮球从离地面1m高处竖直下落,与地相碰后,被反向弹回至0.9m高处.在这一过程中,皮球经过的路程和位移大小分别为( )
| A. | 1.9m,1.9m | B. | 1m,0.9m | C. | 1.9m,0.9m | D. | 1.9m,0.1m |
10. 如图一木块放在水平桌面上,在水平外力F2=3N,F1=8N和作用下处于静止状态,若撤去力F1,则木块在水平方向受到的摩擦力为( )
如图一木块放在水平桌面上,在水平外力F2=3N,F1=8N和作用下处于静止状态,若撤去力F1,则木块在水平方向受到的摩擦力为( )
 如图一木块放在水平桌面上,在水平外力F2=3N,F1=8N和作用下处于静止状态,若撤去力F1,则木块在水平方向受到的摩擦力为( )
如图一木块放在水平桌面上,在水平外力F2=3N,F1=8N和作用下处于静止状态,若撤去力F1,则木块在水平方向受到的摩擦力为( )| A. | 8N、向左 | B. | 8N、向左 | C. | 3N、向右 | D. | 3N、向左 |
20.一质点做匀变速直线运动,通过A点时的速度为vA,经过时间t通过B点时速度为vB,再经过相同时间t通过C点时速度为vC,则关于物体通过B点时的速度vB和物体的加速度a的关系式,正确的是( )
| A. | vB=$\frac{{v}_{A}+{v}_{C}}{2}$ | B. | vB=$\frac{AB+BC}{2t}$ | C. | a=$\frac{{v}_{C}-{v}_{A}}{2t}$ | D. | a=$\frac{BC-AB}{4{t}^{2}}$ |
7.关于互成角度的两个初速度不为零的匀变速直线运动的合运动,下列说法正确的( )
| A. | 合运动的轨迹一定是抛物线 | |
| B. | 合运动的性质一定是匀变速运动 | |
| C. | 合运动一定是匀变速直线运动 | |
| D. | 任意相等时间间隔△t内合速度的增量一定相等 |
4.将一张纸条平放在水平桌面上,在纸条的上面竖直立一笔帽,把纸条从笔帽下抽出,如果缓慢拉动纸条,笔帽必倒;如果快速拉出纸条,笔帽有可能不倒.对于这种现象,下列说法中正确的是( )
| A. | 缓慢抽出纸条,笔帽受到的摩擦力大 | |
| B. | 快速抽出纸条,笔帽受到的摩擦力大 | |
| C. | 缓慢抽出纸条,笔帽受到的冲量大 | |
| D. | 快速抽出纸条,笔帽受到的冲量大 |
 一只装有工件的木箱,质量m=40kg.木箱与水平地面的动摩擦因数μ=0.3,现用200N的斜向右下方的力F推木箱,推力的方向与水平面成θ=30°角,如所示.求木箱的加速度大小.(g取9.8m/s2)
一只装有工件的木箱,质量m=40kg.木箱与水平地面的动摩擦因数μ=0.3,现用200N的斜向右下方的力F推木箱,推力的方向与水平面成θ=30°角,如所示.求木箱的加速度大小.(g取9.8m/s2)