题目内容
质点做初速度为零的匀加速直线运动,在前2s内、第二个2s内、第4s内,这三段时间内的位移之比为( )
分析:根据匀变速直线运动的位移时间公式分别求出各段时间内的位移,从而得出位移之比.
解答:解:设质点的加速度为a,则在前2s内的位移x1=
at12=
a×4=2a.
在第二个2s内的位移x2=
at22-
at12=
a×16-
a×4=6a.
在第4s内的位移x3=
at2-
at′2=
a×16-
a×9=
,则x1:x2:x3=4:12:7.故C正确,A、B、D错误.
故选C.
| 1 |
| 2 |
| 1 |
| 2 |
在第二个2s内的位移x2=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
在第4s内的位移x3=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 7a |
| 2 |
故选C.
点评:解决本题的关键掌握匀变速直线运动的运动学公式,并能灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
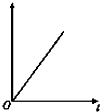 如图所示,是某一质点做直线运动的图象,下列说法中正确的是( )
如图所示,是某一质点做直线运动的图象,下列说法中正确的是( )| A、若纵轴表示速度,横轴表示时间,则质点做匀速直线运动 | B、若纵轴表示位移,横轴表示时间,则质点做匀速直线运动 | C、若纵轴表示速度,横轴表示时间,则质点做初速度为零的匀加速直线运动 | D、若纵轴表示位移,横轴表示时间,则质点做初速度为零的匀加速直线运动 |
质点做初速度为零的匀加速直线运动,由静止开始通过连续三段位移所用时间分别是1s、2s、3s,这三段位移大小之比和这三段位移上的平均速度大小之比分别是( )
| A、1:2:3,1:1:1 | B、1:3:5,1:2:3 | C、12:22:32,12:22:32 | D、13:23:33,12:22:32 |
 如图所示,是一质点做直线运动的图象,下列说法中正确的是( )
如图所示,是一质点做直线运动的图象,下列说法中正确的是( )