题目内容
2009哈尔滨第24届大学生冬季运动会的高山滑雪。有一滑雪坡由AB和BC组成,AB是倾角为37°的斜坡,BC是半径为R=5m的圆弧面,圆弧面和斜面相切于B,与水平面相切于C,如图所示,AB竖直高度差hl=8.8m,竖直台阶CD高度差为h2=5m,台阶底端与倾角为37°斜坡DE相连.运动员连同滑雪装备总质量为80kg,从A点由静止滑下通过C点后飞落到DE上(不计空气阻力和轨道的摩擦阻力,g取10m/s2,sin37°=0.6,cos37°=0.8).求:

(1)运动员到达C点的速度大小;
(2)运动员经过C点时轨道受到的压力大小;
(3)运动员在空中飞行的时间.

(1)运动员到达C点的速度大小;
(2)运动员经过C点时轨道受到的压力大小;
(3)运动员在空中飞行的时间.
:⑴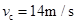 (2)
(2)  (3)
(3) 
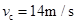 (2)
(2)  (3)
(3) 
解:⑴A→C过程,由动能定理得:
 (4分)
(4分)
 (1分)
(1分)
代入数据解得: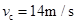 (2分)
(2分)
⑵在C点,由牛顿第二定律有: (3分)
(3分)
解得: ( 1分)
( 1分)
由牛顿第三定律知,运动员在C点时轨道受到的压力大小为3936N.(1分)
(3)运动员在空中做平抛运动,
设飞行时间为t,则水平位移: (1分)
(1分)
竖直位移: (3分)
(3分)
解得 (
( 舍去) (2分)
舍去) (2分)
本题考查的是对牛顿定律和动能定理的应用问题,对运动员进行受力分析,根据动能定理和牛顿第二定律即可求解速度和对轨道的压力,再利用平抛运动的规律解出最后结果。
 (4分)
(4分) (1分)
(1分) 代入数据解得:
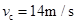 (2分)
(2分)⑵在C点,由牛顿第二定律有:
 (3分)
(3分)解得:
 ( 1分)
( 1分)由牛顿第三定律知,运动员在C点时轨道受到的压力大小为3936N.(1分)
(3)运动员在空中做平抛运动,
设飞行时间为t,则水平位移:
 (1分)
(1分)竖直位移:
 (3分)
(3分)解得
 (
( 舍去) (2分)
舍去) (2分)本题考查的是对牛顿定律和动能定理的应用问题,对运动员进行受力分析,根据动能定理和牛顿第二定律即可求解速度和对轨道的压力,再利用平抛运动的规律解出最后结果。

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目


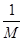 的图线
的图线
 圆周轨道,其A端与圆心等高,B端在圆心的正下方,已知轨道半径R=1.0m,一个质量m=1.0kg的小物体自A端由静止开始沿轨道下滑,当它滑到B点时,它对B点的压力N=19N,求小物体沿轨道下滑过程中滑动摩擦力所做的功。(g取10m/s2)
圆周轨道,其A端与圆心等高,B端在圆心的正下方,已知轨道半径R=1.0m,一个质量m=1.0kg的小物体自A端由静止开始沿轨道下滑,当它滑到B点时,它对B点的压力N=19N,求小物体沿轨道下滑过程中滑动摩擦力所做的功。(g取10m/s2)


