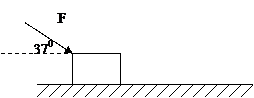题目内容
 如图所示,一个静止在水平面地面上的质量为2kg物体,在8N的水平恒力作用下,以2m/s2的加速度从静止开始沿水平地面向右运动,求:
如图所示,一个静止在水平面地面上的质量为2kg物体,在8N的水平恒力作用下,以2m/s2的加速度从静止开始沿水平地面向右运动,求:(1)物体在3s末的速度;
(2)物体在3s内发生的位移;
(3)物体与地面间的摩擦力大小.
分析:(1)物体做匀加速直线运动,速度由公式v=at求解.
(2)物体在3s内发生的位移由公式x=
at2求解.
(3)根据牛顿第二定律求解摩擦力.
(2)物体在3s内发生的位移由公式x=
| 1 |
| 2 |
(3)根据牛顿第二定律求解摩擦力.
解答:解:(1)物体在3s末的速度为 v=at=2×3m/s=6m/s;
(2)物体在3s内发生的位移为 x=
at2=
×2×32m=9m;
(3)设物体与地面间的摩擦力大小为f.根据牛顿第二定律得:
F-f=ma
则得:f=F-ma=(8-2×2)N=4N
答:
(1)物体在3s末的速度是6m/s;
(2)物体在3s内发生的位移是9m;
(3)物体与地面间的摩擦力大小是4N.
(2)物体在3s内发生的位移为 x=
| 1 |
| 2 |
| 1 |
| 2 |
(3)设物体与地面间的摩擦力大小为f.根据牛顿第二定律得:
F-f=ma
则得:f=F-ma=(8-2×2)N=4N
答:
(1)物体在3s末的速度是6m/s;
(2)物体在3s内发生的位移是9m;
(3)物体与地面间的摩擦力大小是4N.
点评:解答本题关键掌握运动学的速度公式和位移公式,以及牛顿第二定律,常见的基础题.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目