题目内容
5.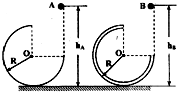 如图所示,两个$\frac{3}{4}$圆弧轨道固定在水平地面上,半径R相同,A轨道由金属凹槽制成,B轨道由金属圆管制成,均可视为光滑轨道.在两轨道右侧的正上方分别将金属小球A和B由静止释放,小球距离地面的高度分别用hA和hB表示,则下列说法正确的( )
如图所示,两个$\frac{3}{4}$圆弧轨道固定在水平地面上,半径R相同,A轨道由金属凹槽制成,B轨道由金属圆管制成,均可视为光滑轨道.在两轨道右侧的正上方分别将金属小球A和B由静止释放,小球距离地面的高度分别用hA和hB表示,则下列说法正确的( )| A. | 若hA=hB≥2R,则两小球都能沿轨道运动到最高点 | |
| B. | 若hA=hB=$\frac{3R}{2}$,由于机械能守恒,两个小球沿轨道上升的最大高度均为$\frac{3R}{2}$ | |
| C. | 适当调整hA和hB,均可使两小球从轨道最高点飞出后,恰好落在轨道右端口处 | |
| D. | 若使小球沿轨道运动并且从最高点飞出,A小球的最小高度为$\frac{5R}{2}$,B小球在hB>2R的任何高度均可 |
分析 小球A恰好能到A轨道的最高点时,轨道对小球无作用力,由重力提供小球的向心力,由牛顿第二定律求出速度.小球恰好能到B轨道的最高点时,速度为零,根据机械能守恒分别求出hA和hB.再判断hA=hB=2R,两小球是否能沿轨道运动到最高点.根据最高点的临界速度求出小球最高点飞出的水平位移的最小值.
解答 解:AD、A球最高点最小速度为 v=$\sqrt{gR}$,则由机械能守恒定律可知,mg(hA-2R)=$\frac{1}{2}$mvA2,A球下落的最小高度为$\frac{5}{2}$R;而B中小球只要在最高点的速度大于2R即可;故A错误,D正确;
B、若hA=hB=$\frac{3R}{2}$,由上分析知,A球在到达最高点前离开轨道,离开轨道时有速度,由机械能守恒可知:mg$\frac{3R}{2}$=mgh+$\frac{1}{2}mv{′}^{2}$,v′>0,则h<$\frac{3}{2}$R.
对于B球,由机械能守恒可知:mg$\frac{3R}{2}$=mgh,得h=$\frac{3}{2}$R.故B错误.
C、小球A能从A飞出的最小速度为v=$\sqrt{gR}$,从最高点飞出后下落R高度时,水平位移的最小值为:xA=vt=$\sqrt{gR}$•$\sqrt{\frac{2R}{g}}$=$\sqrt{2}$R>R,则小球A落在轨道右端口外侧.而适当调整hB,B可以落在轨道右端口处.故C错误;
故选:D
点评 本题是向心力、机械能守恒定律、平抛运动的综合,A轨道与轻绳系的球模型相似,B轨道与轻杆固定的球模型相似,要注意临界条件的不同.

练习册系列答案
相关题目
20.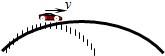 如图所示,圆弧形桥面半径L,汽车以一定的速度V (V<$\sqrt{gL}$)经过桥面的顶点时,关于汽车的受力及汽车对桥面的压力情况,以下说法正确的是( )
如图所示,圆弧形桥面半径L,汽车以一定的速度V (V<$\sqrt{gL}$)经过桥面的顶点时,关于汽车的受力及汽车对桥面的压力情况,以下说法正确的是( )
 如图所示,圆弧形桥面半径L,汽车以一定的速度V (V<$\sqrt{gL}$)经过桥面的顶点时,关于汽车的受力及汽车对桥面的压力情况,以下说法正确的是( )
如图所示,圆弧形桥面半径L,汽车以一定的速度V (V<$\sqrt{gL}$)经过桥面的顶点时,关于汽车的受力及汽车对桥面的压力情况,以下说法正确的是( )| A. | 在竖直方向汽车受到三个力:重力和桥面的支持力和向心力 | |
| B. | 在竖直方向汽车只受两个力,重力和桥面的支持力 | |
| C. | 汽车对桥面的压力小于汽车的重力 | |
| D. | 汽车对桥面的压力大于汽车的重力 |
1.将水平弹簧振子从其平衡位置O拉开到位置A然后自由释放.若OA距离增大,则下列判断中正确的是( )
| A. | 振动的位移要大些 | B. | 振动的周期要长些 | ||
| C. | 振动的频率要大些 | D. | 振动的能量要大些 |
10.关于曲线运动,下列说法中正确的是( )
| A. | 某点的速度方向为该点切线方向 | B. | 曲线运动一定是变速运动 | ||
| C. | 物体的速度方向时刻改变 | D. | 曲线运动可能是匀速运动 |
15.关于重力的叙述,下列说法中正确的是( )
| A. | 物体的质量越大,受到的重力也越大,所以物体的重力是由物体的质量产生的 | |
| B. | 重力是物体本身的一种属性 | |
| C. | 放在支撑面上的物体受到的重力的方向总是垂直向下的 | |
| D. | 物体的重力是由于地球对它的吸引而产生的 |

 如图所示,质量为M的木板静止在足够长的光滑水平台面上,一质量为m的物块(可视为质点)在细线的水平拉力作用下,以速度v从木板的最左端滑上,并一直以该速度运动,已知物块与木板间的动摩擦因数为μ,物块最远只能向右到达木板的中间位置,且此时木板的右端距离平台的最右端(定滑轮所在处)还很远,求:
如图所示,质量为M的木板静止在足够长的光滑水平台面上,一质量为m的物块(可视为质点)在细线的水平拉力作用下,以速度v从木板的最左端滑上,并一直以该速度运动,已知物块与木板间的动摩擦因数为μ,物块最远只能向右到达木板的中间位置,且此时木板的右端距离平台的最右端(定滑轮所在处)还很远,求: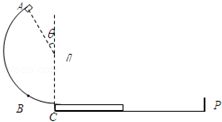 如图所示,ABC是半径R=m的光滑圆弧轨道,A点和圆弧圆心O的连线与竖直方向的夹角θ=37°,C端在圆弧轨道圆心O的正下方,现在某一位置水平抛出一个质量m=2kg的小滑块(可视为质点),并恰好从轨道的上端A点以速度vA=4m/s沿圆弧切线进入轨道,从轨道末端C点滑上了与它等高的足够长的木板,小物块与木板间的动摩擦因数μ=0.5,水平面光滑且右边有竖直的挡板P,挡板P与C间的距离足够远,设长木板与挡板P碰撞无机械能损失,长木板的质量M=1kg.(g取10m/s2),试求:
如图所示,ABC是半径R=m的光滑圆弧轨道,A点和圆弧圆心O的连线与竖直方向的夹角θ=37°,C端在圆弧轨道圆心O的正下方,现在某一位置水平抛出一个质量m=2kg的小滑块(可视为质点),并恰好从轨道的上端A点以速度vA=4m/s沿圆弧切线进入轨道,从轨道末端C点滑上了与它等高的足够长的木板,小物块与木板间的动摩擦因数μ=0.5,水平面光滑且右边有竖直的挡板P,挡板P与C间的距离足够远,设长木板与挡板P碰撞无机械能损失,长木板的质量M=1kg.(g取10m/s2),试求: