题目内容
 (附加题)如图甲所示,一边长L=2.5m、质量m=0.5kg的正方形金属线框,放在光滑绝缘的水平面上,整个装置放在方向竖直向上、磁感应强度B=0.8T的匀强磁场中,它的一边与磁场的边界MN重合.在水平力F作用下由静止开始向左运动,经过5s线框被拉出磁场.测得金属线框中的电流随时间变化的图象如乙图所示,在金属线框被拉出的过程中.
(附加题)如图甲所示,一边长L=2.5m、质量m=0.5kg的正方形金属线框,放在光滑绝缘的水平面上,整个装置放在方向竖直向上、磁感应强度B=0.8T的匀强磁场中,它的一边与磁场的边界MN重合.在水平力F作用下由静止开始向左运动,经过5s线框被拉出磁场.测得金属线框中的电流随时间变化的图象如乙图所示,在金属线框被拉出的过程中.(1)求通过线框导线截面的电量及线框的电阻;
(2)写出水平力F随时间变化的表达式;
(3)已知在这5s内力F做功1.92J,那么在此过程中,线框产生的焦耳热是多少?
【答案】分析:(1)电流随时间线性变化,可知平均电流,根据q=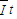 ,求出通过导线框截面的电量.根据法拉第电磁感应定律
,求出通过导线框截面的电量.根据法拉第电磁感应定律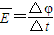 ,
,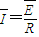 ,求出电阻.
,求出电阻.
(2)根据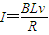 ,结合电流随时间的变化规律,得出速度随时间的变化规律,从而求出加速度,根据牛顿第二定律,求出水平外力F随时间的变化关系.
,结合电流随时间的变化规律,得出速度随时间的变化规律,从而求出加速度,根据牛顿第二定律,求出水平外力F随时间的变化关系.
(3)求出5s末的速度,根据能量守恒求出线框中产生的焦耳热.
解答:解:(1)根据q=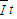 ,由I-t图象得,q=1.25C
,由I-t图象得,q=1.25C
又根据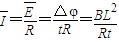
得R=4Ω.
(2)由电流图象可知,感应电流随时间变化的规律:I=0.1t
由感应电流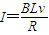 ,可得金属框的速度随时间也是线性变化的,
,可得金属框的速度随时间也是线性变化的,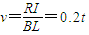
线框做匀加速直线运动,加速度a=0.2m/s2.
线框在外力F和安培力FA作用下做匀加速直线运动,F-FA=ma
得F=(0.2t+0.1)N
(3)t=5s时,线框从磁场中拉出时的速度v5=at=1m/s
由能量守恒得: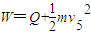
线框中产生的焦耳热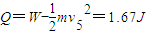
点评:解决本题的关键掌握电动势的两个表达式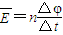 ,E=BLv.以及熟练运用能量守恒定律.
,E=BLv.以及熟练运用能量守恒定律.
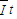 ,求出通过导线框截面的电量.根据法拉第电磁感应定律
,求出通过导线框截面的电量.根据法拉第电磁感应定律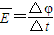 ,
,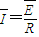 ,求出电阻.
,求出电阻.(2)根据
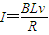 ,结合电流随时间的变化规律,得出速度随时间的变化规律,从而求出加速度,根据牛顿第二定律,求出水平外力F随时间的变化关系.
,结合电流随时间的变化规律,得出速度随时间的变化规律,从而求出加速度,根据牛顿第二定律,求出水平外力F随时间的变化关系.(3)求出5s末的速度,根据能量守恒求出线框中产生的焦耳热.
解答:解:(1)根据q=
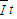 ,由I-t图象得,q=1.25C
,由I-t图象得,q=1.25C又根据
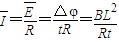
得R=4Ω.
(2)由电流图象可知,感应电流随时间变化的规律:I=0.1t
由感应电流
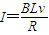 ,可得金属框的速度随时间也是线性变化的,
,可得金属框的速度随时间也是线性变化的,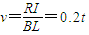
线框做匀加速直线运动,加速度a=0.2m/s2.
线框在外力F和安培力FA作用下做匀加速直线运动,F-FA=ma
得F=(0.2t+0.1)N
(3)t=5s时,线框从磁场中拉出时的速度v5=at=1m/s
由能量守恒得:
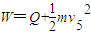
线框中产生的焦耳热
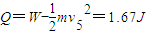
点评:解决本题的关键掌握电动势的两个表达式
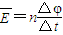 ,E=BLv.以及熟练运用能量守恒定律.
,E=BLv.以及熟练运用能量守恒定律. 
练习册系列答案
相关题目
 (2013?青浦区一模)(附加题)如图甲所示,一边长L=2.5m、质量m=0.5kg的正方形金属线框,放在光滑绝缘的水平面上,整个装置放在方向竖直向上、磁感应强度B=0.8T的匀强磁场中,它的一边与磁场的边界MN重合.在水平力F作用下由静止开始向左运动,经过5s线框被拉出磁场.测得金属线框中的电流随时间变化的图象如乙图所示,在金属线框被拉出的过程中.
(2013?青浦区一模)(附加题)如图甲所示,一边长L=2.5m、质量m=0.5kg的正方形金属线框,放在光滑绝缘的水平面上,整个装置放在方向竖直向上、磁感应强度B=0.8T的匀强磁场中,它的一边与磁场的边界MN重合.在水平力F作用下由静止开始向左运动,经过5s线框被拉出磁场.测得金属线框中的电流随时间变化的图象如乙图所示,在金属线框被拉出的过程中.
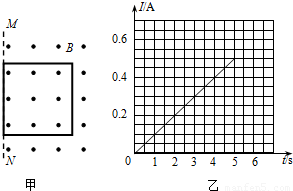 (附加题)如图甲所示,一边长L=2.5m、质量m=0.5kg的正方形金属线框,放在光滑绝缘的水平面上,整个装置放在方向竖直向上、磁感应强度B=0.8T的匀强磁场中,它的一边与磁场的边界MN重合.在水平力F作用下由静止开始向左运动,经过5s线框被拉出磁场.测得金属线框中的电流随时间变化的图象如乙图所示,在金属线框被拉出的过程中.
(附加题)如图甲所示,一边长L=2.5m、质量m=0.5kg的正方形金属线框,放在光滑绝缘的水平面上,整个装置放在方向竖直向上、磁感应强度B=0.8T的匀强磁场中,它的一边与磁场的边界MN重合.在水平力F作用下由静止开始向左运动,经过5s线框被拉出磁场.测得金属线框中的电流随时间变化的图象如乙图所示,在金属线框被拉出的过程中.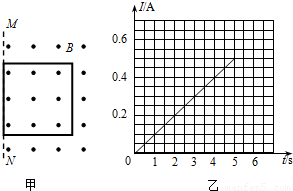 (附加题)如图甲所示,一边长L=2.5m、质量m=0.5kg的正方形金属线框,放在光滑绝缘的水平面上,整个装置放在方向竖直向上、磁感应强度B=0.8T的匀强磁场中,它的一边与磁场的边界MN重合.在水平力F作用下由静止开始向左运动,经过5s线框被拉出磁场.测得金属线框中的电流随时间变化的图象如乙图所示,在金属线框被拉出的过程中.
(附加题)如图甲所示,一边长L=2.5m、质量m=0.5kg的正方形金属线框,放在光滑绝缘的水平面上,整个装置放在方向竖直向上、磁感应强度B=0.8T的匀强磁场中,它的一边与磁场的边界MN重合.在水平力F作用下由静止开始向左运动,经过5s线框被拉出磁场.测得金属线框中的电流随时间变化的图象如乙图所示,在金属线框被拉出的过程中.