题目内容
19.质子和α粒子由静止开始经同一电场加速后,沿垂直于磁感线方向进入同一匀强磁场,则质子和α粒子在磁场中各运动参量之间的关系为( )| A. | 速度之比为$\sqrt{2}:1$ | B. | 周期之比为1:2 | ||
| C. | 向心力之比为$\sqrt{2}:1$ | D. | 运动半径之比为$\sqrt{2}:1$ |
分析 根据动能定理求出粒子进入磁场的速度,根据洛伦兹力公式求解洛伦兹力之比,结合粒子在磁场中运动的半径公式和周期公式求出周期之比和半径之比.
解答 解:A、由动能定理得:qU=$\frac{1}{2}$mv2-0,解得:$v=\sqrt{\frac{2qU}{m}}$,因为质子和α粒子的电量之比为1:2,质量之比为1:4,则速率之比为$\sqrt{2}$:1,故A正确.
B、粒子在磁场中运动的周期:$T=\frac{2πm}{qB}$,因为质子和α粒子的电量之比为1:2,质量之比为1:4,则周期之比为1:2,故B正确.
C、洛伦兹力提供向心力,故:f=Fn=qvB=$qB\sqrt{\frac{2qU}{m}}$,因为质子和α粒子的电量之比为1:2,质量之比为1:4,则洛伦兹力之比为1:$\sqrt{2}$,故C错误;
D、粒子在磁场中运动的半径$r=\frac{mv}{qB}$,速度$v=\sqrt{\frac{2qU}{m}}$,故r=$\frac{1}{B}\sqrt{\frac{2mU}{q}}$,因为质子和α粒子的电量之比为1:2,质量之比为1:4,则半径之比为1:$\sqrt{2}$,故D错误;
故选:AB
点评 解决本题的关键掌握粒子在磁场中的半径公式和周期公式,并能灵活运用,注意在计算题中,半径公式和周期公式不能直接运用.

练习册系列答案
相关题目
10.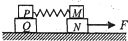 如图所示,光滑水平面上放置从M、N、P、Q四个木块,其中P、M质量均为m,N、Q质量均为2m,从P之间用一轻质弹簧相连.现用水平拉力F拉N,使四个木块以同一加速度a向右运动,则在突然撤去F瞬间,下列说法正确的是( )
如图所示,光滑水平面上放置从M、N、P、Q四个木块,其中P、M质量均为m,N、Q质量均为2m,从P之间用一轻质弹簧相连.现用水平拉力F拉N,使四个木块以同一加速度a向右运动,则在突然撤去F瞬间,下列说法正确的是( )
 如图所示,光滑水平面上放置从M、N、P、Q四个木块,其中P、M质量均为m,N、Q质量均为2m,从P之间用一轻质弹簧相连.现用水平拉力F拉N,使四个木块以同一加速度a向右运动,则在突然撤去F瞬间,下列说法正确的是( )
如图所示,光滑水平面上放置从M、N、P、Q四个木块,其中P、M质量均为m,N、Q质量均为2m,从P之间用一轻质弹簧相连.现用水平拉力F拉N,使四个木块以同一加速度a向右运动,则在突然撤去F瞬间,下列说法正确的是( )| A. | PQ间的摩擦力不变 | B. | M、P的加速度大小变为$\frac{1}{2}$a | ||
| C. | MN间的摩擦力不变 | D. | N的加速度大小仍为a |
7. 如图所示,PQ、MN是放置在水平面内的光滑导轨,GH是长度为L、电阻为r的导体棒,其中点与一端固定的轻弹簧连接,轻弹簧的劲度系数为k.导体棒处在方向向下、磁感应强度为B的匀强电场中.图中E是电动势为E,内阻不计的直流电源,电容器的电容为C.闭合开关,待电路稳定后,下列选项错误的是( )
如图所示,PQ、MN是放置在水平面内的光滑导轨,GH是长度为L、电阻为r的导体棒,其中点与一端固定的轻弹簧连接,轻弹簧的劲度系数为k.导体棒处在方向向下、磁感应强度为B的匀强电场中.图中E是电动势为E,内阻不计的直流电源,电容器的电容为C.闭合开关,待电路稳定后,下列选项错误的是( )
 如图所示,PQ、MN是放置在水平面内的光滑导轨,GH是长度为L、电阻为r的导体棒,其中点与一端固定的轻弹簧连接,轻弹簧的劲度系数为k.导体棒处在方向向下、磁感应强度为B的匀强电场中.图中E是电动势为E,内阻不计的直流电源,电容器的电容为C.闭合开关,待电路稳定后,下列选项错误的是( )
如图所示,PQ、MN是放置在水平面内的光滑导轨,GH是长度为L、电阻为r的导体棒,其中点与一端固定的轻弹簧连接,轻弹簧的劲度系数为k.导体棒处在方向向下、磁感应强度为B的匀强电场中.图中E是电动势为E,内阻不计的直流电源,电容器的电容为C.闭合开关,待电路稳定后,下列选项错误的是( )| A. | 导体棒中电流为 $\frac{E}{{R}_{2}+r{+R}_{1}}$ | B. | 轻弹簧的长度增加 $\frac{BLE}{k(r{+R}_{1})}$ | ||
| C. | 轻弹簧的长度减少 $\frac{BLE}{k(r{+R}_{1})}$ | D. | 电容器带电量为 $\frac{E}{r{+R}_{1}}$CR |
4.学习物理除了知识的学习外,还要领悟并掌握处理物理问题的思想与方法以及相关的物理学史.下列关于物理学中的思想方法及物理学史实的叙述中正确的是( )
| A. | 伽利略最早是在其论著《时间简史》中提出了对古希腊哲人亚里士多德关于物体下落的速度与物体受到的重力成正比的错误观点的批判 | |
| B. | 伽利略最早是在其论著《两种科学的对话》中提出了对古希腊哲人亚里士多德关于物体下落的速度与物体受到的重力成正比的错误观点的批判 | |
| C. | 在探究滑动摩擦力大小的决定因素时采用了等效替代法 | |
| D. | 伽利略在研究力与运动关系时利用了理想实验法 |
11.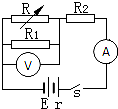 如图所示的电路中,电源电动势为E,内阻为r.若调整可变电阻R的阻值,可使电压表的示数减小△U,电流表示数变化△I,两电表均为理想电表,在这个过程中( )
如图所示的电路中,电源电动势为E,内阻为r.若调整可变电阻R的阻值,可使电压表的示数减小△U,电流表示数变化△I,两电表均为理想电表,在这个过程中( )
 如图所示的电路中,电源电动势为E,内阻为r.若调整可变电阻R的阻值,可使电压表的示数减小△U,电流表示数变化△I,两电表均为理想电表,在这个过程中( )
如图所示的电路中,电源电动势为E,内阻为r.若调整可变电阻R的阻值,可使电压表的示数减小△U,电流表示数变化△I,两电表均为理想电表,在这个过程中( )| A. | R2两端的电压增加,增加量一定等于△U | |
| B. | 电阻箱的阻值一定减小,电流表示数一定增大 | |
| C. | △U-△I•R2=△I•r | |
| D. | $\frac{△U}{△I}=r+{R_2}$ |
8.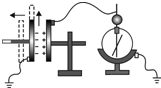 用控制变量法,可以研究影响平行板电容器电容的因素(如图),设两极板正对面积为S,极板间的距离为d,静电计指针偏角为θ.实验中,极板所带电荷量不变,若( )
用控制变量法,可以研究影响平行板电容器电容的因素(如图),设两极板正对面积为S,极板间的距离为d,静电计指针偏角为θ.实验中,极板所带电荷量不变,若( )
 用控制变量法,可以研究影响平行板电容器电容的因素(如图),设两极板正对面积为S,极板间的距离为d,静电计指针偏角为θ.实验中,极板所带电荷量不变,若( )
用控制变量法,可以研究影响平行板电容器电容的因素(如图),设两极板正对面积为S,极板间的距离为d,静电计指针偏角为θ.实验中,极板所带电荷量不变,若( )| A. | 保持S不变,增大d,则θ变大 | B. | 保持S不变,增大d,则θ变小 | ||
| C. | 保持d不变,增大S,则θ变大 | D. | 若在两极间增加介质,则θ变小 |
 (共10分,选择题4分,填充、画图各2分.)在“探究求合力的方法”的实验过程中,完成下列三个问题:
(共10分,选择题4分,填充、画图各2分.)在“探究求合力的方法”的实验过程中,完成下列三个问题: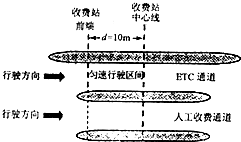 2015年9月28日,内蒙古、黑龙江、广西、新疆四省正式加入高速公路电子不停车收费(ETC)联网系统.至此,高速公路ETC系统基本实现全国联网(西藏、海南除外).汽车驶离高速公路时.分别通过ETC通道和人工收费通道的流程如图所示.假设汽车到达收费站前端时速度为v1=5m/s,如果过ETC通道,只需匀速通过中心线后,再匀加速至V2=15m/s后正常行驶;如果过人工收费通道,从前端开始匀减速至中心线处速度恰好为0,经过T=20s缴费成功后,再启动汽车匀加速至v2正常行驶.已知收费站前端和中心线间的距离d=10m,设汽车加速过程中的加速度大小为a=2m/s2,求汽车从进入收费站前端到再次加速到v2.
2015年9月28日,内蒙古、黑龙江、广西、新疆四省正式加入高速公路电子不停车收费(ETC)联网系统.至此,高速公路ETC系统基本实现全国联网(西藏、海南除外).汽车驶离高速公路时.分别通过ETC通道和人工收费通道的流程如图所示.假设汽车到达收费站前端时速度为v1=5m/s,如果过ETC通道,只需匀速通过中心线后,再匀加速至V2=15m/s后正常行驶;如果过人工收费通道,从前端开始匀减速至中心线处速度恰好为0,经过T=20s缴费成功后,再启动汽车匀加速至v2正常行驶.已知收费站前端和中心线间的距离d=10m,设汽车加速过程中的加速度大小为a=2m/s2,求汽车从进入收费站前端到再次加速到v2. 如图所示,重力为G1=10N,G2=20N的木块悬挂在绳PC和PB的结点上,PB水平,G2在倾角为30°的斜面上,PA偏离竖直方向30°,系统处于静止.试求:
如图所示,重力为G1=10N,G2=20N的木块悬挂在绳PC和PB的结点上,PB水平,G2在倾角为30°的斜面上,PA偏离竖直方向30°,系统处于静止.试求: