题目内容
20.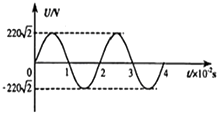 如图为一正弦交变电压随时间变化的图象.由图可知:
如图为一正弦交变电压随时间变化的图象.由图可知:①交变电压最大值为220$\sqrt{2}$V.有效值为220V.
②交表电压的周期为0.02S.频率是50HZ.
③交变电压角速度为:100πrad/s.
④交变电压的瞬时值表达式:U=U=220$\sqrt{2}$sin100πt V.
分析 根据图象可读出该交流电的周期和最大值,然后根据频率和周期,最大值与有效值的关系可直接求解.
解答 解:①由图象读出电压的最大值Um=220$\sqrt{2}$V,则有效值为:U=$\frac{220\sqrt{2}}{\sqrt{2}}$=220V,
②由图象读出交表电压的周期为T=0.02S,频率是f=$\frac{1}{T}$=50
③由图象知周期T=0.02s,线圈转动的角速度为:ω=$\frac{2π}{0.02}$=100πrad/s,
④交变电压瞬时值表达式:U=220$\sqrt{2}$sin100πt V
故答案为:①220$\sqrt{2}$; 220
②0.02;50
③100π
④U=220$\sqrt{2}$sin100πt V
点评 要能根据图象获取有用信息,并能利用这些信息进行有关运算,知道最大值与有效值的关系.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
4.精彩的F1赛事相信你不会陌生吧!车王舒马赫在2005年以8000万美元的年收入高居全世界所有运动员榜首.在观众感觉精彩与刺激的同时,车手们却时刻处在紧张与危险之中.这位车王在一个弯道上突然高速行驶的赛车后轮脱落,从而不得不遗憾地退出了比赛.关于脱落的后轮的运动情况,以下说法正确的是( )
| A. | 仍然沿着汽车行驶的弯道运动 | |
| B. | 沿着与弯道垂直的方向飞出 | |
| C. | 沿着脱离时,轮子前进的方向做直线运动,离开弯道 | |
| D. | 上述情况都有可能 |
8.假设火星可视为质量均匀分布的球体,已知“火卫一”(火星的卫星)绕火星做圆周运动的半径为R,周期为T,火星的半径为R0,自转周期为T0,则火星表面的重力加速度在赤道处大小与两极处大小的比值为( )
| A. | $\frac{{R}^{3}{T}_{0}^{2}}{{R}_{0}^{3}{T}^{2}}$ | B. | $\frac{{R}_{0}^{3}{T}^{2}}{{R}^{3}{T}_{0}^{2}}$ | ||
| C. | 1-$\frac{{R}^{3}{T}_{0}^{2}}{{R}_{0}^{3}{T}^{2}}$ | D. | 1-$\frac{{R}_{0}^{3}{T}^{2}}{{R}^{3}{T}_{0}^{2}}$ |
9.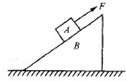 如图所示,斜面体B放在水平地面上,木块A放在斜面体B上,用一个沿斜面向上的力F拉木块A,在力F的作用下,物体A与斜面体B一起沿水平方向匀速移动,已知斜面倾角为θ,则关于斜面体B受力的个数,下面说法中正确的是( )
如图所示,斜面体B放在水平地面上,木块A放在斜面体B上,用一个沿斜面向上的力F拉木块A,在力F的作用下,物体A与斜面体B一起沿水平方向匀速移动,已知斜面倾角为θ,则关于斜面体B受力的个数,下面说法中正确的是( )
 如图所示,斜面体B放在水平地面上,木块A放在斜面体B上,用一个沿斜面向上的力F拉木块A,在力F的作用下,物体A与斜面体B一起沿水平方向匀速移动,已知斜面倾角为θ,则关于斜面体B受力的个数,下面说法中正确的是( )
如图所示,斜面体B放在水平地面上,木块A放在斜面体B上,用一个沿斜面向上的力F拉木块A,在力F的作用下,物体A与斜面体B一起沿水平方向匀速移动,已知斜面倾角为θ,则关于斜面体B受力的个数,下面说法中正确的是( )| A. | 可能是3个 | B. | 可能是4个 | C. | 可能是5个 | D. | 一定是5个 |
10.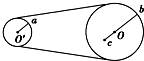 如图所示的皮带传动中,小轮半径ra是大轮半径rb的一半,大轮上c点到轮心O的距离恰等于ra,若皮带不打滑,则图中a、b、c三点( )
如图所示的皮带传动中,小轮半径ra是大轮半径rb的一半,大轮上c点到轮心O的距离恰等于ra,若皮带不打滑,则图中a、b、c三点( )
 如图所示的皮带传动中,小轮半径ra是大轮半径rb的一半,大轮上c点到轮心O的距离恰等于ra,若皮带不打滑,则图中a、b、c三点( )
如图所示的皮带传动中,小轮半径ra是大轮半径rb的一半,大轮上c点到轮心O的距离恰等于ra,若皮带不打滑,则图中a、b、c三点( )| A. | 线速度之比为2:1:1 | B. | 角速度之比为2:1:1 | ||
| C. | 转动周期之比为2:1:1 | D. | 向心加速度大小之比为4:2:1 |
 如图,在0≤x≤$\sqrt{3}$a区域内存在与xy平面垂直的匀强磁场,磁感强强度的大小为B.在t=0时刻,一位于坐标原点的粒子源在xy平面内发射出大量同种带电粒子,所有粒子的初速度大小相同,方向与y轴正方向的夹角分布在0-180°范围内.已知沿y轴正方向发射的粒子在t=t0时刻刚好从磁场边界上P($\sqrt{3}$a,a)点离开磁场.求:
如图,在0≤x≤$\sqrt{3}$a区域内存在与xy平面垂直的匀强磁场,磁感强强度的大小为B.在t=0时刻,一位于坐标原点的粒子源在xy平面内发射出大量同种带电粒子,所有粒子的初速度大小相同,方向与y轴正方向的夹角分布在0-180°范围内.已知沿y轴正方向发射的粒子在t=t0时刻刚好从磁场边界上P($\sqrt{3}$a,a)点离开磁场.求: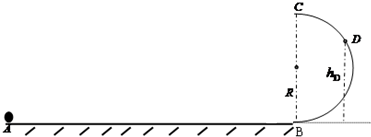
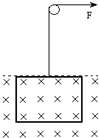 如图所示,某矩形线圈长为L、宽为d、匝数为n、总质量为M,其电阻为R,线圈所在磁场的磁感应强度为B,最初时刻线圈的上边缘与有界磁场上边缘重合,若将线圈从磁场中以速度v匀速向上拉出,则:
如图所示,某矩形线圈长为L、宽为d、匝数为n、总质量为M,其电阻为R,线圈所在磁场的磁感应强度为B,最初时刻线圈的上边缘与有界磁场上边缘重合,若将线圈从磁场中以速度v匀速向上拉出,则: 做描绘小灯泡L的伏安特性曲线实验,已知该灯泡的额定电流为0.5A,最大阻值约为9Ω.提供的备用器材有:
做描绘小灯泡L的伏安特性曲线实验,已知该灯泡的额定电流为0.5A,最大阻值约为9Ω.提供的备用器材有: