题目内容
如图甲,直筒A连同固定在直筒底部的竖直杆的总质量为M=50kg.直筒内部高度H=13.75m;另有一质量为m=2kg的小铁环B套在细杆上,从细杆的底部以v=20m/s的初速度开始向上运动且刚好能到达箱顶;已知小铁环与杆之间的滑动摩擦力大小恒为f=10N,不计空气阻力,g取10m/s2,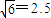 .求:
.求:(1)直筒内细杆长h为多少?
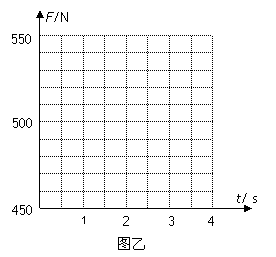
(2)在图乙给定的坐标中,画出铁环从筒底开始上升到第一次返回到筒底的过程中直筒对地面的压力大小F随时间变化的图象(写出简要推算步骤,计算结果小数点后取一位)
(3)若铁环与筒底每次碰撞都没有能量损失,求小环从开始运动到最终停止在筒底,所走过的总路程是多少?
【答案】分析:(1)根据动能定理研究小铁环从细杆的底部以一定的初速度开始向上运动且刚好能到达箱顶的过程求解细杆长度.
(2)分析铁环从筒底开始上升到第一次返回到筒底的过程,运用运动学规律求出各段过程对应的时间.
对直筒进行受力分析,根据平衡条件求出各段过程中直筒对地面的压力大小.
(3)根据动能定理求出小环反弹后第二次假设能升到杆顶需要的初动能,与小环在杆底实际的动能对比判断小环能否越过杆顶.再由动能定理求解所走过的总路程.
解答:
解:(1)根据动能定理研究小铁环从细杆的底部以一定的初速度开始向上运动且刚好能到达箱顶的过程得:
-mgH-fs=0- mv2
mv2
h=12.5m
(2)设第一次沿杆上升到达杆顶用时t1,速度为v1:
小铁环从杆顶到达箱顶做一段匀减速运动,到达箱顶速度为零.
根据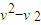 =2ax得:
=2ax得:
v1=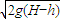 =5.0m/s
=5.0m/s
根据匀变速直线运动规律x=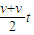 得
得
t1=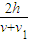 =1.0s
=1.0s
第一次离开杆顶到返回杆顶用时t2:
t2=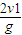 =1.0s
=1.0s
第一次从杆顶滑到杆底速度为v2,沿杆下滑用时t3:
由动能定理研究小环从箱顶到杆底的过程:mgH-fh= mv22
mv22
v2=5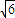 m/s=12.3m/s
m/s=12.3m/s
t3=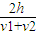 =(
=(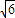 -1)s=1.5s
-1)s=1.5s
隔离直筒,对其受力分析,根据平衡条件和牛顿第三定律得:
直筒对地面的压力大小F分别为:
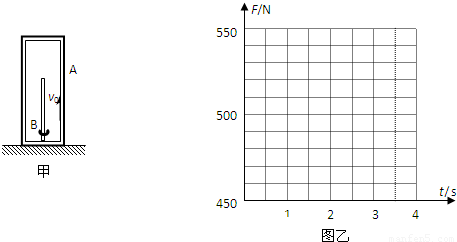
0~1.0s:→F1=Mg-f=490N
1.0s~2.0s→F2=Mg=500N
2.0s~3.5s→F3=Mg+f=510N
如图.
(3)小环反弹后第二次能升到杆顶在杆底所需要的初动能
Ek0=mgh+fh=2×10×12.5+10×12.5=375J
小环第一次滑到杆底的动能为EK2
EK2= m
m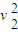 =150.0J
=150.0J
可知:EK2<Ek0
所以小环只能越过杆顶一次,
设小环在杆上反复滑行的总路程为s,由动能定理:
-fs=- m
m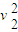 得:s=15.0m
得:s=15.0m
总路程:s′=2H+s=42.5m
答:(1)直筒内细杆长h为12.5m,
(2)见上图
(3)小环从开始运动到最终停止在筒底,所走过的总路程是42.5m.
点评:了解研究对象的运动过程是解决问题的前提,根据题目已知条件和求解的物理量选择物理规律解决问题.
一个题目可能需要选择不同的过程多次运用动能定理研究.
(2)分析铁环从筒底开始上升到第一次返回到筒底的过程,运用运动学规律求出各段过程对应的时间.
对直筒进行受力分析,根据平衡条件求出各段过程中直筒对地面的压力大小.
(3)根据动能定理求出小环反弹后第二次假设能升到杆顶需要的初动能,与小环在杆底实际的动能对比判断小环能否越过杆顶.再由动能定理求解所走过的总路程.
解答:

解:(1)根据动能定理研究小铁环从细杆的底部以一定的初速度开始向上运动且刚好能到达箱顶的过程得:
-mgH-fs=0-
 mv2
mv2 h=12.5m
(2)设第一次沿杆上升到达杆顶用时t1,速度为v1:
小铁环从杆顶到达箱顶做一段匀减速运动,到达箱顶速度为零.
根据
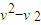 =2ax得:
=2ax得:v1=
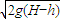 =5.0m/s
=5.0m/s 根据匀变速直线运动规律x=
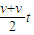 得
得t1=
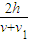 =1.0s
=1.0s 第一次离开杆顶到返回杆顶用时t2:
t2=
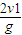 =1.0s
=1.0s 第一次从杆顶滑到杆底速度为v2,沿杆下滑用时t3:
由动能定理研究小环从箱顶到杆底的过程:mgH-fh=
 mv22
mv22v2=5
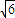 m/s=12.3m/s
m/s=12.3m/s t3=
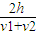 =(
=(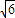 -1)s=1.5s
-1)s=1.5s 隔离直筒,对其受力分析,根据平衡条件和牛顿第三定律得:
直筒对地面的压力大小F分别为:
0~1.0s:→F1=Mg-f=490N
1.0s~2.0s→F2=Mg=500N
2.0s~3.5s→F3=Mg+f=510N
如图.
(3)小环反弹后第二次能升到杆顶在杆底所需要的初动能
Ek0=mgh+fh=2×10×12.5+10×12.5=375J
小环第一次滑到杆底的动能为EK2
EK2=
 m
m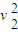 =150.0J
=150.0J 可知:EK2<Ek0
所以小环只能越过杆顶一次,
设小环在杆上反复滑行的总路程为s,由动能定理:
-fs=-
 m
m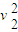 得:s=15.0m
得:s=15.0m 总路程:s′=2H+s=42.5m
答:(1)直筒内细杆长h为12.5m,
(2)见上图
(3)小环从开始运动到最终停止在筒底,所走过的总路程是42.5m.
点评:了解研究对象的运动过程是解决问题的前提,根据题目已知条件和求解的物理量选择物理规律解决问题.
一个题目可能需要选择不同的过程多次运用动能定理研究.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
 如图1示,箱子A连同固定在箱子底部的竖直杆的总质量为M=10kg.箱子内部高度H=3.75m,杆长h=2.5m,另有一质量为m=2kg的小铁环B套在杆上,从杆的底部以v0=10m/s的初速度开始向上运动,铁环B刚好能到达箱顶,不计空气阻力,g取10m/s2.求:
如图1示,箱子A连同固定在箱子底部的竖直杆的总质量为M=10kg.箱子内部高度H=3.75m,杆长h=2.5m,另有一质量为m=2kg的小铁环B套在杆上,从杆的底部以v0=10m/s的初速度开始向上运动,铁环B刚好能到达箱顶,不计空气阻力,g取10m/s2.求: