题目内容
10.设想在月球表面上,宇航员测出小物块自由下落高度h所用时间为t.当飞船在靠近月球表面圆轨道上飞行时,测得其环绕周期是T,已知引力常量G,根据上述各量求.(1)月球表面的重力加速度.
(2)月球的密度.
分析 根据位移时间公式求出月球表面的重力加速度.
根据万有引力提供向心力求出月球的质量,结合月球的体积求出月球的密度.
解答 解:(1)根据h=$\frac{1}{2}g{t}^{2}$得,月球表面的重力加速度为:g=$\frac{2h}{{t}^{2}}$.
(2)根据$G\frac{Mm}{{R}^{2}}=mR\frac{4{π}^{2}}{{T}^{2}}$得月球的质量为:M=$\frac{4{π}^{2}{R}^{3}}{G{T}^{2}}$,
则月球的密度为:ρ=$\frac{M}{V}=\frac{\frac{4{π}^{2}{R}^{3}}{G{T}^{2}}}{\frac{4}{3}π{R}^{3}}$=$\frac{3π}{G{T}^{2}}$.
答:(1)月球表面的重力加速度为$\frac{2h}{{t}^{2}}$;
(2)月球的密度为$\frac{3π}{G{T}^{2}}$.
点评 解决本题的关键掌握万有引力提供向心力这一重要理论,并能灵活运用.基础题.

练习册系列答案
相关题目
4.以下计时数据指的是时间的是( )
| A. | 中央电视台新闻联播节目每天19时开播 | |
| B. | 2011年9月29日21时16分“天宫一号”在酒泉卫星发射中心发射升空 | |
| C. | 足球比赛上下半场各45分钟 | |
| D. | 在某场足球赛中,甲队于开赛9分26秒时攻入一球 |
2. 将横截面积为S的玻璃管弯成如图所示的连通器,放在水平桌面上,左、右管处在竖直状态,先关闭阀门K,往左、右管中分别注入高度为h2、h1,密度为ρ的液体,然后打开阀门K,直到液体静止,重力对液体做的功为( )
将横截面积为S的玻璃管弯成如图所示的连通器,放在水平桌面上,左、右管处在竖直状态,先关闭阀门K,往左、右管中分别注入高度为h2、h1,密度为ρ的液体,然后打开阀门K,直到液体静止,重力对液体做的功为( )
 将横截面积为S的玻璃管弯成如图所示的连通器,放在水平桌面上,左、右管处在竖直状态,先关闭阀门K,往左、右管中分别注入高度为h2、h1,密度为ρ的液体,然后打开阀门K,直到液体静止,重力对液体做的功为( )
将横截面积为S的玻璃管弯成如图所示的连通器,放在水平桌面上,左、右管处在竖直状态,先关闭阀门K,往左、右管中分别注入高度为h2、h1,密度为ρ的液体,然后打开阀门K,直到液体静止,重力对液体做的功为( )| A. | ρgs(h2-h1) | B. | $\frac{1}{4}$ρgs(h2-h1) | C. | $\frac{1}{4}$ρgs(h2-h1)2 | D. | $\frac{1}{2}$ρgs(h2-h1)2 |
15. 2011年1月11日12时50分,歼20在成都实现首飞,历时18分钟,这标志着我国隐形战斗机的研制工作掀开了新的一页.如图所示,隐形战斗机在竖直平面内作横8字形飞行表演,飞行轨迹为1→2→3→4→5→6→1,如果飞行员体重为G,飞行圆周半径为R,速率恒为v,在A、B、C、D四个位置上,飞机座椅和保险带对飞行员的作用力分别为FNA、FNB、FNC、FND,关于这四个力的大小关系正确的是( )
2011年1月11日12时50分,歼20在成都实现首飞,历时18分钟,这标志着我国隐形战斗机的研制工作掀开了新的一页.如图所示,隐形战斗机在竖直平面内作横8字形飞行表演,飞行轨迹为1→2→3→4→5→6→1,如果飞行员体重为G,飞行圆周半径为R,速率恒为v,在A、B、C、D四个位置上,飞机座椅和保险带对飞行员的作用力分别为FNA、FNB、FNC、FND,关于这四个力的大小关系正确的是( )
 2011年1月11日12时50分,歼20在成都实现首飞,历时18分钟,这标志着我国隐形战斗机的研制工作掀开了新的一页.如图所示,隐形战斗机在竖直平面内作横8字形飞行表演,飞行轨迹为1→2→3→4→5→6→1,如果飞行员体重为G,飞行圆周半径为R,速率恒为v,在A、B、C、D四个位置上,飞机座椅和保险带对飞行员的作用力分别为FNA、FNB、FNC、FND,关于这四个力的大小关系正确的是( )
2011年1月11日12时50分,歼20在成都实现首飞,历时18分钟,这标志着我国隐形战斗机的研制工作掀开了新的一页.如图所示,隐形战斗机在竖直平面内作横8字形飞行表演,飞行轨迹为1→2→3→4→5→6→1,如果飞行员体重为G,飞行圆周半径为R,速率恒为v,在A、B、C、D四个位置上,飞机座椅和保险带对飞行员的作用力分别为FNA、FNB、FNC、FND,关于这四个力的大小关系正确的是( )| A. | FNA=FNB<FNC=FND | B. | FNA=FNB>FNC=FND | C. | FNC>FNA=FNB>FND | D. | FND>FNA=FNB=FNC |
19. 在如图所示的电路中,电源的负极接地,其电动势为E、内电阻为r,R1、R2为定值电阻,R3为滑动变阻器,C为电容器,A、V为理想电流表和理想电压表.在滑动变阻器滑动头P自a端向b端滑动的过程中,下列说法中正确的是( )
在如图所示的电路中,电源的负极接地,其电动势为E、内电阻为r,R1、R2为定值电阻,R3为滑动变阻器,C为电容器,A、V为理想电流表和理想电压表.在滑动变阻器滑动头P自a端向b端滑动的过程中,下列说法中正确的是( )
 在如图所示的电路中,电源的负极接地,其电动势为E、内电阻为r,R1、R2为定值电阻,R3为滑动变阻器,C为电容器,A、V为理想电流表和理想电压表.在滑动变阻器滑动头P自a端向b端滑动的过程中,下列说法中正确的是( )
在如图所示的电路中,电源的负极接地,其电动势为E、内电阻为r,R1、R2为定值电阻,R3为滑动变阻器,C为电容器,A、V为理想电流表和理想电压表.在滑动变阻器滑动头P自a端向b端滑动的过程中,下列说法中正确的是( )| A. | 电压表示数变小 | B. | 电流表示数变小 | ||
| C. | a点的电势升高 | D. | 电容器C所带电荷量减少 |
20.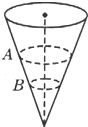 如图所示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,则( )
如图所示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,则( )
 如图所示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,则( )
如图所示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,则( )| A. | 球A的线速度必定小于球B的线速度 | |
| B. | 球A的角速度必定大于球B的角速度 | |
| C. | 球A的运动周期必定小于球B的运动周期 | |
| D. | 球A对筒壁的压力必定等于球B对筒壁的压力 |
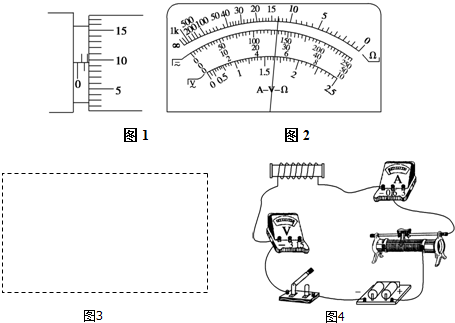
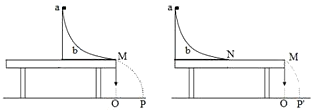 为了测定滑块与桌面之间的动摩擦因数,某同学设计了如图所示的实验装置.其中,a是质量为m的滑块(可视为质点),b是可以固定于桌面的滑槽(滑槽末端与桌面相切).第一次实验时,将滑槽固定于水平桌面的右端,滑槽的末端与桌面的右端M对齐,让滑块a从滑槽上最高点由静止释放滑下,落在水平地面上的P点;第二次实验时,将滑槽固定于水平桌面的左端,测出滑槽的末端N 与桌面的右端M的距离为L,让滑块a再次从滑槽上最高点由静止释放滑下,落在水平地面上的P′点.已知当地重力加速度为g,不计空气阻力.
为了测定滑块与桌面之间的动摩擦因数,某同学设计了如图所示的实验装置.其中,a是质量为m的滑块(可视为质点),b是可以固定于桌面的滑槽(滑槽末端与桌面相切).第一次实验时,将滑槽固定于水平桌面的右端,滑槽的末端与桌面的右端M对齐,让滑块a从滑槽上最高点由静止释放滑下,落在水平地面上的P点;第二次实验时,将滑槽固定于水平桌面的左端,测出滑槽的末端N 与桌面的右端M的距离为L,让滑块a再次从滑槽上最高点由静止释放滑下,落在水平地面上的P′点.已知当地重力加速度为g,不计空气阻力.