题目内容
两个绕太阳运行的行星质量分别为m1和m2，轨道半径分别为r1和r2，若它们只受太阳引力的作用，则这两个行星的向心加速度之比为（ ）
| A、1：1 | ||||
| B、m2r1：m1r2 | ||||
| C、m1r2：m2r1 | ||||
D、r
|
分析：根据万有引力提供向心力得出向心加速度与轨道半径的关系，从而得出向心加速度之比．
解答：解：根据G
=ma得，a=
．因为两行星的轨道半径之比为r1：r2，则两行星的向心加速度之比为r
：r
．故D正确，A、B、C错误．
故选：D．
| Mm |
| r2 |
| GM |
| r2 |
2 2 |
2 1 |
故选：D．
点评：解决本题的关键掌握万有引力提供向心力这一理论，知道线速度、角速度、向心加速度、周期与轨道半径的关系，与环绕天体的质量无关．
练习册系列答案
相关题目
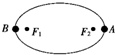某行星绕太阳运行的椭圆轨道如图所示，F1和F2是椭圆轨道的两个焦点，行星在A点的速率比在B点的速率大，则太阳是位于（ ）
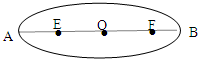某行星绕太阳运行的椭圆轨道如图所示，E和F 是椭圆轨道的两个焦点，行星在A点的速度比在B点的速度大，则太阳位于（ ）