题目内容
 如图所示,从光滑的
如图所示,从光滑的| 1 |
| 4 |
(1)小球运动到
| 1 |
| 4 |
(2)若要使小球滑出槽口后不沿半球面下滑,则R1与R2应满足什么关系?
(3)若小球刚好不沿半球面下滑,则小球落地时的动能为多少?
分析:(1)根据机械能守恒定律求出小球滑出槽口时速度,在槽口根据向心力公式列式即可求解;
(2)若要使小球滑出槽口后不沿半球面下滑,可知重力恰好或不足以提供向心力而作平抛运动;
(3)根据机械能守恒定律即可求解.
(2)若要使小球滑出槽口后不沿半球面下滑,可知重力恰好或不足以提供向心力而作平抛运动;
(3)根据机械能守恒定律即可求解.
解答:解:(1)小球滑出槽口时速度为v,
根据机械能守恒定律得:mgR1=
mv2①
在槽口时:N-mg=m
②
由①②式解得:N=3mg
由牛顿第三定律得:N′=N=3mg 方向:竖直向下
(2)若要使小球滑出槽口后不沿半球面下滑,可知重力恰好或不足以提供向心力而作平抛运动.
即mg≤m
③
由①③两式联立解得R1与R2应满足的关系是:
R1≥
R2
(3)由机械能守恒得:Ek=
mv2+mgR2=
mgR2
答:(1)小球运动到
圆弧槽的底部对圆弧槽的底部压力为3mg,方向竖直向下;
(2)若要使小球滑出槽口后不沿半球面下滑,则R1与R2应满足R1≥
R2;
(3)若小球刚好不沿半球面下滑,则小球落地时的动能为
mgR2.
根据机械能守恒定律得:mgR1=
| 1 |
| 2 |
在槽口时:N-mg=m
| v2 |
| R1 |
由①②式解得:N=3mg
由牛顿第三定律得:N′=N=3mg 方向:竖直向下
(2)若要使小球滑出槽口后不沿半球面下滑,可知重力恰好或不足以提供向心力而作平抛运动.
即mg≤m
| v2 |
| R2 |
由①③两式联立解得R1与R2应满足的关系是:
R1≥
| 1 |
| 2 |
(3)由机械能守恒得:Ek=
| 1 |
| 2 |
| 3 |
| 2 |
答:(1)小球运动到
| 1 |
| 4 |
(2)若要使小球滑出槽口后不沿半球面下滑,则R1与R2应满足R1≥
| 1 |
| 2 |
(3)若小球刚好不沿半球面下滑,则小球落地时的动能为
| 3 |
| 2 |
点评:本题关键根据机械能守恒定律和向心力公式列式,同时要注意在最低点,重力不足于提供绕半球运动所需的向心力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
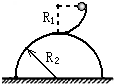
 如图所示,从光滑的1/4圆弧槽的最高点滑下的小球,滑出槽口时速度为水平方向,槽口与一个半球顶点相切,半球底面为水平,若要使小球滑出槽口后不沿半球面下滑.已知圆弧槽的半径为R1,半球的半径为R2,则R1与R2应满足什么关系?
如图所示,从光滑的1/4圆弧槽的最高点滑下的小球,滑出槽口时速度为水平方向,槽口与一个半球顶点相切,半球底面为水平,若要使小球滑出槽口后不沿半球面下滑.已知圆弧槽的半径为R1,半球的半径为R2,则R1与R2应满足什么关系?
 B.
B. C.
C. D.
D.



 B.
B. C.
C. D.
D.

 B.
B.
 D.
D.