题目内容
（2007?扬州模拟）地球和月亮可以看作是一个“双星”系统，它们都绕着同一点0做匀速圆周运动．已知地球质量是月亮质量的8l倍，地球球心与月亮球心之问的距离是地球半径R的60倍．则0点距地球球心的距离为（ ）
分析：这是一个“双星”的问题，地球和月球围绕它们连线上的同一点O分别做匀速圆周运动，它们之间的万有引力提供各自的向心力，周期和角速度相等，根据牛顿第二定律分别对地球和月球列式，即可求得0点距地球球心的距离．
解答：解：设地球和月球绕O点做匀速圆周运动的角速度为ω，O点到地球球心和月球球心的距离分别为r1和r2．
根据牛顿第二定律得：
对地球：G
=m地ω2r1…①
对月球：G
=m月ω2r2…②
由①：②得：
=
=
又r1+r2=60R
解得：r1=
R
故选D
根据牛顿第二定律得：
对地球：G
| m地m月 |
| (60R)2 |
对月球：G
| m地m月 |
| (60R)2 |
由①：②得：
| r1 |
| r2 |
| m月 |
| m地 |
| 1 |
| 81 |
又r1+r2=60R
解得：r1=
| 30 |
| 41 |
故选D
点评：本题是双星模型，与卫星绕地球运动模型不同，两颗星都绕同一圆心做匀速圆周运动，关键抓住条件：相同的角速度和周期．
练习册系列答案
英才计划期末调研系列答案
精英口算卡系列答案
相关题目
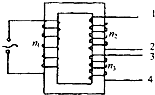（2007?扬州模拟）如图所示，一个有两个不同副线圈的理想变压器，原线圈匝数为nl=1100匝，两剐线圈的匝 数分别为n2=20匝和n3=70匝．原线圈接入220V交变电压，今将一额定电压为1OV的用电器接入变压器的副线圈输出端后能正常工作，则两个副线圈连接方式应是（ ）
（2007?扬州模拟）如图甲所示，带电粒子（不计重力）以水平向右的初速度v0先通过有界匀强电场E，后通过有界匀强磁场B，再从磁场右边穿出，此过程中该粒子动能的改变量为E1；若如图乙所示，将该匀强电场和匀强磁场区域正交叠加，再让该粒子以同样的初速度水平向右穿越叠加场区而从右边穿出，此过程中该粒子动能的改变量为E2．比较场强的大小，下列说法中正确的是（ ）