题目内容

如图是小车做匀变速直线运动而当到的一条纸带，所用电源的频率是50Hz，图中A、B、C、D、E、F等是按时间顺序先后打出的记数点（每两个记数点间有四个实验点未画出）．用刻度尺量出AB、EF之间距离分别为2.40cm和0.84cm，那么对应打B点时小车的瞬时速度是
0.26
0.26
m/s，小车的加速度大小是
0.39
0.39
m/s2，方向是
由F到A
由F到A
（填“由A到F”或“由F到A”）（结果保留两位有效数字）
分析：根据某段时间内的平均速度等于中间时刻的瞬时速度求出AB段中间时刻的瞬时速度，从而根据速度时间公式求出B点的速度．根据连续相等时间内的位移之差是一恒量，求出小车的加速度大小和方向．
解答：解：根据xEF-xAB=4aT2得，
a=
xEF-xAB
4T2
=
(0.84-2.40)×10-2
4×0.01
m/s2=-0.39m/s2，
负号表示方向，方向为由F到A．
AB段的平均速度等于v=
xAB
T
=
2.40×10-2
0.1
m/s=0.24m/s，
则B点的速度vB=v-a
T
2
=0.24+0.39×0.05m/s≈0.26m/s．
故答案为：0.26，0.39，由F到A．
点评：解决本题的关键掌握纸带的处理，会通过纸带求解瞬时速度和加速度．
练习册系列答案
相关题目
如图所示，小车上有一根固定的水平横杆，横杆左端固定的轻杆与竖直方向成θ角，轻杆下端连接一小铁球；横杆右端用一根细线悬挂一小铁球，当小车做匀变速直线运动时，细线保持与竖直方向成α角，若θ＜α，则下列说法中正确的是（　　）
（1）在“探究速度随时间变化的规律”实验中，小车做匀变速直线运动，记录小车运动的纸带如图1所示．某同学在纸带上共选择7个计数点A、B、C、D、E、F、G，打点计时器每0.02s打一个点，相邻两个计数点之间还有4个点没有画出．他量得各点到A点的距离如图1所示．则：

①本实验中所使用的交流电源的频率为
50
50
Hz；
②打B点时小车的速度vB=
0.25
0.25
m/s，BE间的平均速度
.
V
BE=
0.40
0.40
m/s．
③纸带的加速度a=
1.00
1.00
m/s2．（计算结果保留小数点后两位）．
（2）某同学用如图2所示的实验装置来验证“力的平行四边形定则”．弹簧测力计A挂于固定点P，下端用细线挂一重物M．弹簧测力计B的一端用细线系于O点，手持另一端向左拉，使结点O静止在某位置．分别读出弹簧测力计A和B的示数，并在贴于竖直木板的白 记录O点的位置和拉线的方向．
①本实验用的弹簧测力计示数的单位为N，图中A的示数为
3.6
3.6
N．
②下列不必要的实验要求是
D
D
．（请填写选项前对应的字母）
（A）应测量重物M所受的重力
（B）弹簧测力计应在使用前校零
（C）拉线方向应与木板平面平行
（D）改变拉力，进行多次实验，每次都要使O点静止在同一位置．
（1）如图1是一辆连有纸带的小车做匀变速直线运动时，打点计时器所打的纸带的一部分．打点频率为50Hz，图中A、B、C、D、E、F…是按时间顺序先后确定的计数点（每两个计数点间有四个实验点未画出）．用刻度尺量出AB、DE之间的距离分别是2.40cm和0.84cm．
①那么小车的加速度大小是
0.52
0.52
m/s2，方向与小车运动的方向相
反
反
．

②若当时电网中交变电流的频率变为60Hz，但该同学并不知道，那么做实验的这个同学测得的物体加速度的测量值与实际值相比
偏小
偏小
（选填：“偏大”、“偏小”或“不变”）．（以上各空均保留两位小数）
（2）用频闪照相的方式研究平抛运动，如图2是小球在竖直放置的坐标纸上留下的三个像点，图中每个小方格的边长都是0.54cm，已知闪光频率是30Hz，那么重力加速度g=
9.72
9.72
m/s2，小球的初速度是v0=
0.486
0.486
m/s，（以上各空均保留三位有效数字）
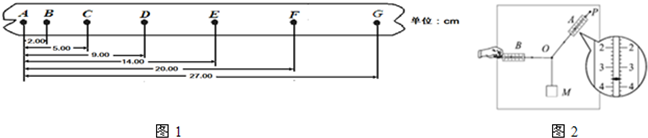
精英家教网如图所示，在车厢内悬线下悬挂一小球m，当小车做匀变速直线运动时，悬线将与竖直方向成某一角度．若在汽车底板上还有一个跟其相对静止的物体m1，则关于汽车的运动情况和物体m1的受力情况正确的是（　　）

如图所示，小车上有一根固定的水平横杆，横杆左端固定的轻杆与竖直方向成θ角，轻杆下端连接一小铁球；横杆右端用一根细线悬挂一小铁球，当小车做匀变速直线运动时，细线保持与竖直方向成α角，若θ<α，则下列说法中正确的是    （    ）

A．轻杆对小球的弹力方向沿着轻杆方向向上

B．轻杆对小球的弹力方向与细线平行向上

C．小车一定以加速度gtgα向右做匀加速运动

D．小车一定以加速度gtgθ向右做匀加速运动

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网