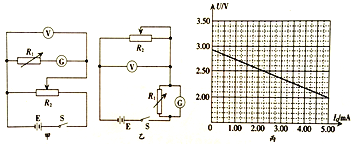
题目内容
【题目】如图所示,宽为L=2m、足够长的金属导轨MN和M′N′放在倾角为θ=30°的斜面上,在N和N′之间连有一个阻值为R=1.2Ω的电阻,在导轨上AA’处放置一根与导轨垂直、质量为m=0.8kg、电阻为r=0.4Ω的金属滑杆,导轨的电阻不计.用轻绳通过定滑轮将电动小车与滑杆的中点相连,绳与滑杆的连线平行于斜面,开始时小车位于滑轮的正下方水平面上的P处(小车可视为质点),滑轮离小车的高度H=4.0m.在导轨的NN′和OO′所围的区域存在一个磁感应强度B=1.0T、方向垂直于斜面向上的匀强磁场,此区域内滑杆和导轨间的动摩擦因数为μ=![]() ,此区域外导轨是光滑的.电动小车沿PS方向以v=1.0m/s的速度匀速前进时,滑杆经d=1m的位移由AA′滑到OO′位置.(g取10m/s2)求:
,此区域外导轨是光滑的.电动小车沿PS方向以v=1.0m/s的速度匀速前进时,滑杆经d=1m的位移由AA′滑到OO′位置.(g取10m/s2)求:

(1)请问滑杆AA′滑到OO′位置时的速度是多大?
(2)若滑杆滑到OO′位置时细绳中拉力为10.1N,滑杆通过OO′位置时的加速度?
(3)若滑杆运动到OO′位置时绳子突然断了,则从断绳到滑杆回到AA′位置过程中,电阻R上产生的热量Q为多少?(设导轨足够长,滑杆滑回到AA’时恰好做匀速直线运动.)
【答案】(1)0.6m/s;(2)2m/s2;(3)0.81J.
【解析】
试题(1)由速度分解法求出滑杆AA′滑到OO′位置时的速度;
(2)感应电动势为E=BLv,由欧姆定律求出电流,由安培力公式求出安培力,然后由牛顿第二定律求出加速度.
(3)由平衡条件求出滑杆的速度,由能量守恒定律求出产生的热量.
解:(1)滑杆运动到OO′位置时,小车通过S点时的速度为v=1.0m/s,设系绳与水平面的夹角为α,则![]() ﹣H=d,sinα=0.8,α=53°,
﹣H=d,sinα=0.8,α=53°,
此时向上的速度即绳端沿绳长方向的速度:v1=vcosα=0.6m/s.
(2)滑杆运动到OO’位置产生感应电动势E=BLv1,产生感应电流 I=![]()
受到的安培力 F安=BIL=![]() ,
,
代入数据,可得F安=1.5N.
滑杆通过OO′位置时所受摩擦力 f=μmgcosθ=![]() ×0.8×10×
×0.8×10×![]() =3N.
=3N.
由牛顿第二定律得:F﹣mgsinθ﹣f﹣F安=ma,
解得加速度:a=2m/s2.
(3)设滑杆返回运动到AA′位置后做匀速运动的速度为v2,由平衡条件得:
mgsinθ=μmgcosθ+![]() ,
,
带入数据,可得:v2=0.4m/s
由能量守恒定律得:Q=![]() mv12﹣
mv12﹣![]() mv22+mgdsinθ﹣μmgdcosθ,
mv22+mgdsinθ﹣μmgdcosθ,
带入数据,可得Q=1.08J
电阻R上产生的热量 QR=![]() Q,
Q,
解得:QR=0.81J.
答:(1)滑杆AA′滑到OO′位置时的速度是0.60m/s;
(2)若滑杆滑到OO′位置时细绳中拉力为10.1N,滑杆通过OO′位置时的加速度是2m/s2;
(3)若滑杆运动到OO′位置时绳子突然断了,则从断绳到滑杆回到AA′位置过程中,电阻R上产生的热量Q为0.81J.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案