题目内容
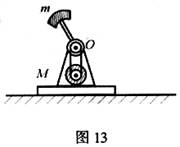如图13是电动打夯机的结构示意图，电动机带动质量为m的重锤(重锤可视为质点)绕转轴O匀速转动，重锤转动半径为R。电动机连同打夯机底座的质量为M,重锤和转轴O之间连接杆的质量可以忽略不计，重力加速度为g。
(1)重锤转动的角速度为多大时，才能使打夯机底座刚好离开地面？
(2)若重锤以上述的角速度转动，当打夯机的重锤通过最低位置时，打夯机对地面的压力为多大？
（1）ω=
（2）2(M+m)g
解析:
(1)重锤在竖直平面内做匀速圆周运动，当重锤运动通过最高点时，打夯机底座受连接杆竖直向上的作用力达到最大。此时重锤所受的重力mg和连接杆对重锤向下的拉力T1提供重锤的向心力，根牛顿第二定律
T1+mg=mw2R。 …………1分
连接杆对打夯机底座向上的拉力 T1′=T1。 …………1分
当T′=Mg时，打夯机底座刚好离开地面， …………1分
解得 ω=
。 …………1分
(2)当重锤通过最低位置时，重锤所受的重力mg和连接杆的拉力T2的合力提供重锤的向心力，根据牛顿第二定有： T2-mg=mw2R。…………1分
连接杆对打夯机底座的作用力T2′的方向向下，且T2′=T2。
设打夯机受到地面的支持力N，根据牛顿第二定律，
N=Mg+T2’ ，…………1分
联立以上各式解得 N=2（M+m）g 。…………1分
根据牛顿第三定律，打夯机对地面压力的大小N′=N=2(M+m)g。…………1分
