题目内容
8.甲车以加速度3m/s2由静止开始作匀加速直线运动,乙车落后2s在同一地点由静止出发,以加速度4m/s2作加速直线运动,两车速度方向一致.在乙车追上甲车之前,两车距离的最大值是( )| A. | 18m | B. | 22m | C. | 24m | D. | 28m |
分析 在速度相等前,乙车的速度小于甲车的速度,两者的距离逐渐增大,在速度相等后,乙车的速度大于甲车的速度,两者的距离逐渐减小,可知两车在速度相等时,相距最远.结合运动学公式求出两者相距的最大距离.
解答 解:设乙车出发后,经过t时间相距最远.
乙车出发时,甲车的速度为6m/s.
则有:a乙t=v0+a甲t,代入数据得,4t=6+3t解得t=6s.
此时甲的位移${x}_{甲}=\frac{1}{2}{a}_{1}(t+2)^{2}=\frac{1}{2}×3×(6+2)^{2}=96$m
乙的位移${x}_{乙}=\frac{1}{2}{a}_{2}{t}^{2}=\frac{1}{2}×4×{6}^{2}=72$.
则两者相距的最大距离△x=x甲-x乙=96-72=24m.故C正确,A、B、D错误.
故选:C.
点评 解决本题的关键知道速度相等时,两者相距最远,结合运动学公式灵活求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.输入端 A、B、C输入信号为何值时,输出端Y输出“1”( )
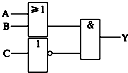

| A. | 0 0 0 | B. | 0 1 1 | C. | 1 0 0 | D. | 1 1 1 |
13. 如图所示,两块相互靠近彼此绝缘的平行金属板组成平行板电容器,极板N与静电计金属球相连,极板M和静电计的外壳均接地.用静电计测量平行板电容器两极板间的电势差U.在两板相距为d时,给电容器充电,静电计指针张开一定角度.在整个实验过程中,保持电容器的带电量Q不变,下面的操作中将使静电计指针张角变小的是( )
如图所示,两块相互靠近彼此绝缘的平行金属板组成平行板电容器,极板N与静电计金属球相连,极板M和静电计的外壳均接地.用静电计测量平行板电容器两极板间的电势差U.在两板相距为d时,给电容器充电,静电计指针张开一定角度.在整个实验过程中,保持电容器的带电量Q不变,下面的操作中将使静电计指针张角变小的是( )
 如图所示,两块相互靠近彼此绝缘的平行金属板组成平行板电容器,极板N与静电计金属球相连,极板M和静电计的外壳均接地.用静电计测量平行板电容器两极板间的电势差U.在两板相距为d时,给电容器充电,静电计指针张开一定角度.在整个实验过程中,保持电容器的带电量Q不变,下面的操作中将使静电计指针张角变小的是( )
如图所示,两块相互靠近彼此绝缘的平行金属板组成平行板电容器,极板N与静电计金属球相连,极板M和静电计的外壳均接地.用静电计测量平行板电容器两极板间的电势差U.在两板相距为d时,给电容器充电,静电计指针张开一定角度.在整个实验过程中,保持电容器的带电量Q不变,下面的操作中将使静电计指针张角变小的是( )| A. | 仅将M板向下平移 | |
| B. | 仅将M板向左平移 | |
| C. | 仅将M板向右平移 | |
| D. | 仅在M、N之间插入云母板(介电常数大于1) |
20.在真空中,有两个点电荷,它们之间的静电力为F.如果将一个电荷的电量增大为原来的3倍,将它们之间的距离减小为原来的$\frac{1}{3}$,它们之间的静电力大小等于( )
| A. | F | B. | 9F | C. | 27F | D. | $\frac{F}{9}$ |
17.铁路转弯处要求设计成外轨比内轨高的斜面,当火车以规定的速度通过弯道时,轮缘对内轨、外轨均无挤压.若某转弯处斜面的倾角为θ,火车的转弯半径为r,重力加速度为g,则火车通过此弯道的规定速度大小为( )
| A. | $\sqrt{grsinθ}$ | B. | $\sqrt{grcosθ}$ | C. | $\sqrt{grtanθ}$ | D. | $\sqrt{grcotθ}$ |