题目内容
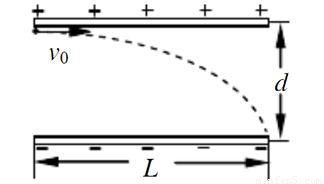
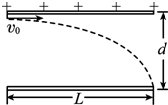 如图所示,两个板长均为L的平板电极平行正对放置,相距为d,极板之间的电势差为U,板间电场可以认为是均匀的.一个质子从正极板边缘以某一初速度垂直于电场方向射入两极板之间,到达负极板时恰好落在极板边缘.已知质子电量为e,质子的质量为m,忽略重力和空气阻力的影响,求:
如图所示,两个板长均为L的平板电极平行正对放置,相距为d,极板之间的电势差为U,板间电场可以认为是均匀的.一个质子从正极板边缘以某一初速度垂直于电场方向射入两极板之间,到达负极板时恰好落在极板边缘.已知质子电量为e,质子的质量为m,忽略重力和空气阻力的影响,求:(1)极板间的电场强度E;
(2)质子的初速度v0.
分析:因为极板间是匀强电场,电场强度直接可根据匀强电场公式求出.质子进入电场后做类平抛运动,在沿电场方向上做初速度为零的匀加速直线运动,在垂直于电场方向上做匀速直线运动.α粒子在极板间运动的加速度a可以根据所受的合力(电场力)求出,α粒子的初速度v0可以根据两分运动的等时性去求解.
解答:解:(1)板间场强为:E=
(2)质子受到的电场力为:F=eE=
质子的加速度为a=
=
α粒子在两板间做类平抛运动
沿初速度方向:L=v0t 垂直于初速度方向:d=
at2
联立解得初速度为v0=
答:(1)极板间的电场强度E=
;
(2)质子的初速度v0=
.
| U |
| d |
(2)质子受到的电场力为:F=eE=
| eU |
| d |
质子的加速度为a=
| F |
| m |
| eU |
| md |
α粒子在两板间做类平抛运动
沿初速度方向:L=v0t 垂直于初速度方向:d=
| 1 |
| 2 |
联立解得初速度为v0=
| L |
| d |
|
答:(1)极板间的电场强度E=
| U |
| d |
(2)质子的初速度v0=
| L |
| d |
|
点评:解决本题关键会对类平抛运动进行分解,注意两分运动的等时性.

练习册系列答案
相关题目
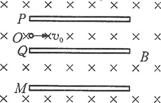
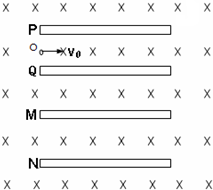 (2007?清远一模)如图所示,两个几何形状完全相同的平行板电容器PQ和MN,水平置于水平方向的匀强磁场中(磁场区域足够大),两电容器极板左端和右端分别在同一竖直线上.已知P、Q之间和M、N之间的距离都是d,板间电压都是U,极板长度均为l.今有一电子从极板左侧的O点以速度v0沿P、Q两板间的中心线进入电容器,并做匀速直线运动穿过电容器,此后经过磁场偏转又沿水平方向进入到电容器M、N板间,在电容器M、N中也沿水平方向做匀速直线运动,穿过M、N板间的电场后,再经过磁场偏转又通过O点沿水平方向进入电容器P、Q极板间,循环往复.已知电子质量为m,电荷为e.
(2007?清远一模)如图所示,两个几何形状完全相同的平行板电容器PQ和MN,水平置于水平方向的匀强磁场中(磁场区域足够大),两电容器极板左端和右端分别在同一竖直线上.已知P、Q之间和M、N之间的距离都是d,板间电压都是U,极板长度均为l.今有一电子从极板左侧的O点以速度v0沿P、Q两板间的中心线进入电容器,并做匀速直线运动穿过电容器,此后经过磁场偏转又沿水平方向进入到电容器M、N板间,在电容器M、N中也沿水平方向做匀速直线运动,穿过M、N板间的电场后,再经过磁场偏转又通过O点沿水平方向进入电容器P、Q极板间,循环往复.已知电子质量为m,电荷为e.