题目内容
如图1所示,在光滑水平面上叠放着甲、乙两物体.现对甲施加水平向右的拉力F,通过传感器可测得甲的加速度a随拉力F变化的关系如图2所示.巳知重力加速度g=10m/s2,由图线可知( )
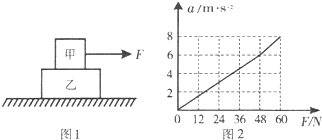

| A、.甲、乙之间的动摩擦因数是0.2 | B、.甲的质量是4kg | C、.甲的质量是2kg | D、甲、乙之间的动摩擦因数是0.6 |
分析:当力F较小时甲乙一起以相同加速度匀加速直线运动,故先用整体法分析;当力F较大时甲乙加速度不同,采用隔离法分析.
解答:解:当F小于某值时,甲乙保持相对静止,一起做匀加速直线运动.当F大于某值时,甲乙开始发生相对滑动.
由图象可以看出当力F<48N时加速度较小,所以甲乙相对静止,
采用整体法,由牛顿第二定律:F=(M+m)a,则a=
F,
可知图中直线的较小斜率的倒数等于M与m质量之和,则M+m=
kg=8kg.
当F>48N时,甲乙发生相对滑动,甲的加速度较大,
采用隔离法,由牛顿第二定律:F-μmg=ma′,则a′=
F-μg
可知图中较大斜率倒数等于甲的质量,即m甲=
kg=6kg,较大斜率直线的延长线与a的截距等于μg,即μg=-2
解得μ=0.2.故A正确,B、C、D错误.
故选:A.
由图象可以看出当力F<48N时加速度较小,所以甲乙相对静止,
采用整体法,由牛顿第二定律:F=(M+m)a,则a=
| 1 |
| M+m |
可知图中直线的较小斜率的倒数等于M与m质量之和,则M+m=
| 48 |
| 6 |
当F>48N时,甲乙发生相对滑动,甲的加速度较大,
采用隔离法,由牛顿第二定律:F-μmg=ma′,则a′=
| 1 |
| m |
可知图中较大斜率倒数等于甲的质量,即m甲=
| 12 |
| 2 |
解得μ=0.2.故A正确,B、C、D错误.
故选:A.
点评:本题考查了牛顿第二定律解决连接体问题,正确的结合图象得出斜率与截距的物理意义是关键.

练习册系列答案
相关题目

 (1)如图1所示,在研究平抛运动时,小球A沿轨道滑下,离开轨道末端(末端水平)时撞开轻质接触式开关S,被电磁铁吸住的小球B同时自由下落.改变整个装置的高度做同样的实验,发现位于同一高度H的A、B两球总是同时落地或者在空中相碰.该实验现象说明了A球在离开轨道后
(1)如图1所示,在研究平抛运动时,小球A沿轨道滑下,离开轨道末端(末端水平)时撞开轻质接触式开关S,被电磁铁吸住的小球B同时自由下落.改变整个装置的高度做同样的实验,发现位于同一高度H的A、B两球总是同时落地或者在空中相碰.该实验现象说明了A球在离开轨道后