题目内容
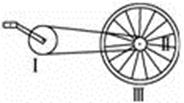
如图所示，两段长为L的轻质线共同系住一个质量为m的小球，另一端分别固定在等高的A、B两点，A、B两点间距也为L。今使小球在竖直面内绕AB水平轴做圆周运动，当小球到达最高点时速率为v，两段线中的拉力恰好为零，若小球到达最高点时速率为2v，则此时每段线中张力大小为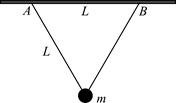
A．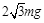
B．
C．3mg D．4mg
B
解析试题分析：当小球到达最高点的速率为v时，两段线中张力恰好均为零，由小球的重力提供向心力，根据牛顿第二定律得出v与半径的关系．若小球到达最高点速率为2v，由重力、两绳拉力的合力提供向心力，由牛顿第二定律得出绳子的拉力与速度、半径的关系，联立求出两绳拉力的合力，再由力的合成法求出每段线中的张力．
当速率为v时，则有mg=m
①，当速率为2v时，则有mg+F=m
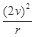②，联立①②得，F=3mg；
设每根线上的张力为T，满足：2Tcos30°=F，解得T=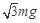
。故本题选B。
考点：牛顿第二定律在圆周运动中的应用，圆周运动中的临界问题，共点力的合成
津桥教育计算小状元系列答案关于匀速圆周运动的线速度、角速度、周期之间的关系，下列说法中正确的是 ( )
| A．线速度大的角速度一定大 |
| B．线速度大的周期一定小 |
| C．角速度大的半径一定小 |
| D．角速度大的周期一定小 |
如图所示，小球A质量为m，固定在长为L的轻细直杆一端，并随杆一起绕杆的另一端O点在竖直平面内做圆周运动，如果小球经过最高位置时速度为
，则杆对球的作用力为（ ）
A．推力， | B．拉力， |
C．推力， | D．拉力， |
公路急转弯处通常是交通事故多发地带。如图，某公路急转弯处是一圆弧，当汽车行驶的速率为vc时，汽车恰好没有向公路内外两侧滑动的趋势，则在该弯道处，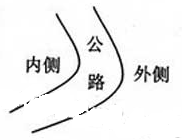
| A．路面外侧高内侧低 |
| B．车速只要低于vc，车辆便会向内侧滑动 |
| C．车速虽然高于vc，但只要不超出某一高度限度，车辆便不会向外侧滑动 |
| D．当路面结冰时，与未结冰时相比，vc的值变小 |
如图所示，一偏心轮绕垂直纸面的轴O匀速转动，a和b是轮上质量相等的两个质点，则偏心轮转动过程中a、b两质点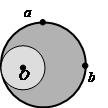 
| A．角速度大小相等 | B．线速度大小相等 |
| C．向心加速度大小相等 | D．向心力大小相等 |
如图所示，在光滑的圆锥面内，两个质量不相同的小球P和Q，沿其内表面在不同的水平面内做半径不同的匀速圆周运动，其中球P的轨道半径较大，则 
| A．球P的角速度较小 | B．球P的向心力较小 |
| C．球P的加速度较大 | D．球P的线速度较大 |
如图所示为质点P、Q做匀速圆周运动的向心加速度随半径变化的图线。表示质点P的图线是过原点的一条直线，表示质点Q的图线是双曲线。由图线可知( )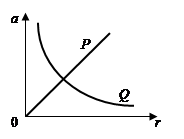
| A．质点P的线速度大小不变 | B．质点P的角速度大小不变 |
| C．质点Q的角速度大小不变 | D．质点Q的周期大小不变 |
