题目内容
【题目】如图所示,在游乐节目中,选手需要借助悬挂在高处的绳飞越到对面的高台上。一质量m=60 kg的选手脚穿轮滑鞋以v0=7m/s的水平速度抓住竖直的绳开始摆动,选手可看作质点,绳子的悬挂点到选手的距离l=6 m。当绳摆到与竖直方向夹角θ=370时,选手放开绳子,不考虑空气阻力和绳的质量。取重力加速度g=l0 m/s2,sin370=0.6.cos 370=0.8。求:
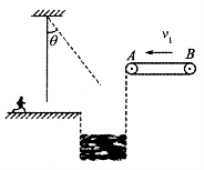
(1)选手放开绳子时的速度大小;
(2)选手放开绳子后继续运动,到最高点时,刚好可以站到水平传送带A点,传送带始终以v=3 m/s的速度匀速向左运动,传送带的另一端B点就是终点,且sAB=3.75 m。若选手在传送带上自由滑行,受到的摩擦阻力为自重的0.2倍。
①通过计算说明该选手是否能顺利冲过终点B。
②求出选手在传送带上滑行过程中因摩擦而产生的热量Q。
【答案】(1)5m/s(2)①选手可以顺利冲过终点B.②990J.
【解析】
试题分析:(1)对选手从抓住绳子到放开绳子的整个过程中,由机械能守恒定律得
![]() mv02=mgL(1-cos37°)+
mv02=mgL(1-cos37°)+![]() mv2;
mv2;
解得:选手放开绳子时的速度 v=5m/s.
(2)①选手在放开绳子时,水平速度为vx,竖直速度为vy,则vx=vcos37°=4m/s.
选手在最高点站到传送带上A点有4m/s向右的速度,在传送带上做匀减速直线运动.
选手的加速度大小![]() .
.
以地面为参考系,由
-vx2=-2ax,
解得 x=4m>3.75m,所以选手可以顺利冲过终点B.
②设选手从A到B的时间为t,则
sAB=vxt-![]() at2;
at2;
解得t1=1.5s,t2=2.5s(舍去)
在这段时间内传送带通过的位移为:x1=v1t=4.5m.
摩擦力做功为:Wf=Q=kmg(sAB+x1)=990J.

 阅读快车系列答案
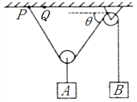
阅读快车系列答案【题目】某同学利用如图所示的气垫导轨装置验证系统机械能守恒定律。在气垫导轨上安装了两光电门1、2,滑块上固定一遮光条,滑块用细线绕过定滑轮与钩码相连.
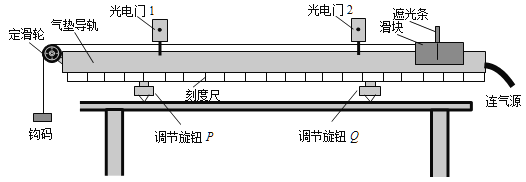
①实验时要调整气垫导轨水平.不挂钩码和细线,接通气源,释放滑块,如果滑块 ,则表示气垫导轨已调整至水平状态.
②不挂钩码和细线,接通气源,滑块从轨道右端向左运动的过程中,发现滑块通过光电门1的时间小于通过光电门2的时间.实施下列措施能够达到实验调整目标的是( )
A.调节P使轨道左端升高一些 |
B.调节Q使轨道右端降低一些 |
C.遮光条的宽度应适当大一些 |
D.滑块的质量增大一些 |
E.气源的供气量增大一些
③实验时,测出光电门1、2间的距离L,遮光条的宽度d,滑块和遮光条的总质量M,钩码质量m.由数字计时器读出遮光条通过光电门1、2的时间t1、t2,则系统机械能守恒成立的表达式是 .