题目内容
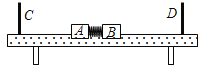
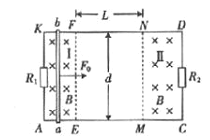
【题目】如图所示，绝缘水平面内固定有一间距d=1 m、电阻不计的足够长光滑矩形导轨AKDC，导轨两端接有阻值分别为R1=3 Ω和R2=6Ω的定值电阻。矩形区域AKFE、NMCD范围内均有方向竖直向下、磁感应强度大小B=lT的匀强磁场I和Ⅱ。一质量m=0．2 kg.电阻r=l Ω的导体棒ab垂直放在导轨上AK与EF之间某处，在方向水平向右、大小F0 =2 N的恒力作用下由静止开始运动，刚要到达EF时导体棒ab的速度大小v1=3 m／s，导体棒ab进入磁场Ⅱ后，导体棒ab中通过的电流始终保持不变。导体棒ab在运动过程中始终保持与导轨垂直且接触良好，空气阻力不计。
(1)求导体棒ab刚要到达EF时的加速度大小a，；
(2)求两磁场边界EF和MN之间的距离L；
(3)若在导体棒ab刚要到达MN时将恒力F0撤去，求导体棒ab能继续滑行的距离s以及滑行该距离s
的过程中整个回路产生的焦耳热Q。
【答案】（1） 5m/s2 （2）1.35m （3） 3.6J
【解析】试题分析：由左手定则可判定安培力方向，再由切割感应电动势，及牛顿第二定律与闭合电路欧姆定律，即可求解； 利用平衡条件，求解导体棒ab进入磁场Ⅱ的速度，再依据牛顿第二定律，及运动学公式，即可求解两磁场边界EF和MN之间的距离；运用牛顿第二定律和闭合电路欧姆定律，结合运动学公式，及微积分求和，与能量守恒定律，即可求解．
（1）导体棒ab刚要到达EF时，在磁场中切割磁感线产生的感应电动势
经分析可知，此时导体棒ab所受安培力的方向水平向左，
由牛顿第二定律，则有：
根据闭合电路的欧姆定律，则有：
，上式中，
解得
；
（2）导体棒ab进入磁场Ⅱ后，受到的安培力与
平衡，做匀速直线运动，
导体棒ab中通过的电流
，保持不变，则有
，其中，
设导体棒ab从EF运动到MN的过程中的加速度大小为
，
根据牛顿第二定律，则有
；
导体棒ab在EF，MN之间做匀加速直线运动，则有：
解得
（3）对撤去后，导体棒ab继续滑行的过程中，
根据牛顿第二定律和闭合电路欧姆定律，则有：
；而
若
，则有：
；
由以上三式可得： 
则有：
，即
，解得：
；
根据能量守恒定律，则有：
因
，代入数据，解得
J
