题目内容
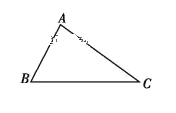
【题目】如图所示,三棱镜ABC三个顶角度数分别为∠A=75°、∠B=60°、∠C=45°,一束频率为5.3×1014 Hz的单色细光束从AB面某点入射,进入棱镜的光线在AC面上发生全反射,离开棱镜BC面时恰好与BC面垂直,已知光在真空中的速度c=3×108 m/s,玻璃的折射率n=1.5,求:
①这束入射光线的入射角的正弦值。
②光在棱镜中的波长。
【答案】①0.75②3.77×10-7m
【解析】
(1)根据光的折射定律,结合几何关系,即可求解;
(2)根据![]() ,求得光在介质中传播速度,再根据v=λf,求得波长,最后根据折射率与临界角的关系,及光路可逆,即可求解。
,求得光在介质中传播速度,再根据v=λf,求得波长,最后根据折射率与临界角的关系,及光路可逆,即可求解。
(1)由光离开棱镜的BC面时恰好与BC面垂直可知,从AB面射到AC面的光线与BC边平行,
设光在AB面的入射角、折射角分别为θ1、θ2,如图所示,
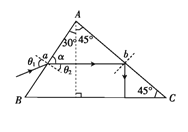
根据几何关系可知θ2=30°
根据折射定律,![]()
得sinθ1=nsinθ2=0.75;
(2)根据![]() 且v=λf
且v=λf
解得:![]() 。
。

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目